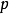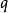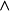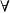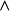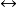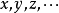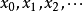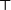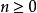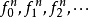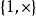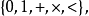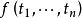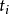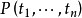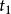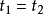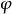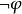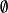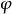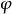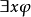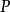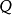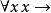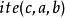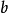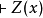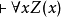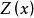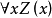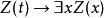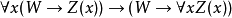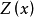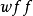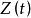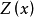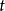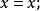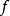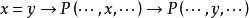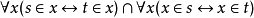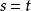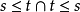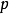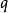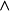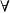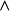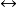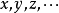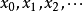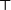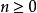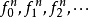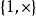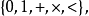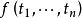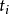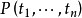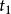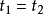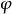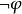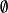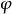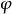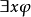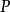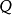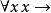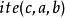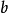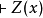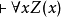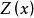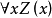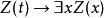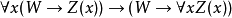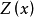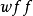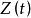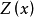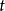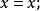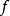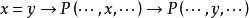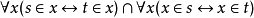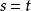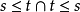基本介紹
- 中文名：一階邏輯
- 外文名：first order logic,FOL
- 別稱：一階謂詞演算
- 套用學科：數學
- 適用領域範圍：數理邏輯
簡介,概念,語法,辭彙表,1.邏輯符號,2.非邏輯符號,生成規則,1.項,2.合成公式,3.推理規則,公理,1.量詞公理,2.等式和它的公理,一階邏輯的元邏輯定理,
簡介
過去一百多年，一階邏輯出現過許多種名稱，包括：一階斷言演算、低階斷言演算、量化理論或斷言邏輯（一個較不精確的用詞）。一階邏輯和命題邏輯的不同之處在於，一階邏輯有使用量化變數。一個一階邏輯，若具有由一系列量化變數、一個以上有意義的斷言字母及包含了有意義的斷言字母的純公理所組成的特定論域，即是一個一階理論。
一階邏輯和其他高階邏輯不同之處在於，高階邏輯的斷言可以有斷言或函式當做引數，且允許斷言量詞或函式量詞的（同時或不同時）存在。在一階邏輯中，斷言通常和集合相關連。在有意義的高階邏輯中，斷言則會被解釋為集合的集合。
存在許多對一階邏輯是可靠（所有可證的敘述皆為真）且完備（所有為真的敘述皆可證）的演繹系統。雖然一階邏輯的邏輯歸結只是半可判定性的，但還是有許多用於一階邏輯上的自動定理證明。一階邏輯也符合一些使其能通過證明論分析的元邏輯定理，如勒文海姆–斯科倫定理及緊緻性定理。
一階邏輯是數學基礎中很重要的一部分，因為它是公理系統的標準形式邏輯。許多常見的公理系統，如一階皮亞諾公理和包含策梅洛-弗蘭克爾集合論的公理化集合論等，都可以形式化成一階理論。然而，一階定理並沒有能力去完整描述及範疇性地建構如自然數或實數之類無限的概念。這些結構的公理系統可以由如二階邏輯之類更強的邏輯來取得。
概念
斷言像是一個會傳回真或偽的函式。考慮下列句子：“蘇格拉底是哲學家”、“柏拉圖是哲學家”。在命題邏輯里，上述兩句被視為兩個不相關的命題，簡單標記為
及
。然而，在一階邏輯里，上述兩句可以使用斷言以更相似的方法來表示。其斷言為
，表示
是哲學家。因此，若
代表蘇格拉底，則 為第一個命題－
；若
代表柏拉圖，則 為第二個命題－q。一階邏輯的一個關鍵要點在此可見：字串“
”為一個語法實體，以當
為哲學家時陳述 為真來賦與其語義。一個語義的賦與稱為解釋。
語法
辭彙表
和英語之類的自然語言不同，一階邏輯的語言是完全形式的，因為可以機械式地判斷一個給定的表示式是否合法。存在兩種合法的表示式：“項”（直觀上代表物件）和“公式”（直觀上代表可真或偽的斷言）。一階邏輯的項與公式是一串符號，這些符號一起形成了這個語言的辭彙表。如同所有的形式語言一般，符號本身的性質不在形式邏輯討論的範圍之內；它們通常只被當成字母及標點符號。
一般會將辭彙表中的符號分成“邏輯符號”（總有相同的意思）及“非邏輯符號”（意思依解釋不同而變動）。例如，邏輯符號
總是解釋成“且”，而絕不會解釋成“或”。另一方面，一個非邏輯斷言符號，如Phil(x) ，可以解釋成“x是哲學家”、“x的個名為Phil的人”或任何其他的1元斷言，單看其解釋為何。
1.邏輯符號
辭彙表中存在若干個邏輯符號，雖然會因作者而異，但通常包括：
1) 量化符號
及
。
2)邏輯聯結詞：或
、且
、條件
、雙條件
及否定
。偶爾還會包括一些其他的邏輯聯結詞。
3) 括弧、方括弧及其他標點符號。此類符號的選擇依文章不同而有所不同。
4) 無限集的變數，通常標記為英文字母末端的小寫字母
，也常會使用下標來區別不同的變數：
。
5)一個等式符號= 。詳見下面的“等式”一節。
需注意，並不是所有的符號都需要，只要有量化符號的其中一個、否定及且、變數、括弧及等式就足夠了。還存在許多定義了額外邏輯符號的變體：
6）有時也會包括真值常數，用T、Vpq或
來表示“真”，並用F、Opq或
來表示“假”。若沒有此類零參數的邏輯算符，這兩個常數就只能用量化來表示。
2.非邏輯符號
非邏輯符號用來表示論域上的斷言（關係）、函式及常數。以前標準上會對所有不同的用途使用相同的無限集的非邏輯符號，而最近則會根據套用的不同而使用不同的非邏輯符號。因此變得需要列舉出使用於一特定套用中的所有非邏輯符號。其選擇是經由標識來形成的。
傳統的做法是對所有的套用都只有單一個無限集的非邏輯符號。因此，根據傳統的做法只會存在一種一階邏輯的語言。這種做法現在依然很常見，尤其是在哲學方面的書籍。
2)對每個整數
，皆存在無限多個
元函式符號：
在當代的數理邏輯里，標識會因套用的不同而不同。數學裡的典型標識，在群里為
或只為
；在序體裡為
。並沒有限制非邏輯符號的數量，標識可以是空的、有限、無限，甚至是不可數的。例如，在勒文海姆–斯科倫定理的證明之中即會出現不可數的標識。
生成規則
生成規則定義一階邏輯的項及公式。因為項及公式被表示為一串符號，這些規則可被用來寫成項及公式的形式文法。這些規則通常是上下文無關的（規則的每個結果在其左側都會有單一個符號），除非允許有無限多符號，且有許多開始符號，如項中的變數。
1.項
項可依如下規則遞歸地定義：
1.變數:每個變數皆是項。
2.函式:每個具有
個參數的表示式
，其中每個參數
是項，且
是具有
個參數的函式符號）是項。另外，常數符號是0參數的函式符號，因此也是項。
只有可經由有限次地套用上述規則來得到的表示式才是項。舉例來說，不存在包含斷言符號的項。
2.合成公式
合式公式可依如下規則遞歸地定義：
1)斷言符號：若
是一個n元斷言符號，且
是項，則
是公式。
2)等式：若等式符號算是邏輯的一部分，且
及
是項，則
是公式。
3)否定：若
是公式，則
是公式。
4)二元聯結詞：若
及 是公式，則
是公式。其他的二元邏輯聯結詞也可相似的規則。
5)量化：若 是公式，且
是變數，則
及
都是公式。
只有可經由有限次地套用上述規則來得到的表示式才是公式。由頭兩個規則得到的公式稱為原子公式。
舉例來說，
定義中的括弧，其用途是為了確保任何公式都只能依遞歸定義以單一種方法得到（換句話說，每一個公式都只存在唯一的剖析樹）。這個性質被稱為公式的唯一可讀性。對於括弧要用在公式中的哪裡存在有許多的慣例。例如，有些作者會使用冒號或句號來代替括弧，或變更括弧插入的地方。但每個作家個人的定義都必須證明會滿足唯一可讀性。
定義公式的規則無法定義“若-則-否則”函式
），其中的
是個以公式表示的條件，當 為真時傳回
，為假時傳回
。這是因為斷言和函式都只能接受項當做其參數，但上述函式的第一個參數為公式。某些建構在一階邏輯上的語言，如SMT-LIB 2.0，會增加此一定義。
3.推理規則
肯定前件充當推理的唯一規則。叫做全稱普遍化的推理規則是斷言演算的特徵。它可以陳述為：
如果
，則
。
這裡的
假定表示斷言演算的一個已證明的定理，而
是它針對於變數x的閉包。斷言字母Z可以被任何斷言字母所替代。
公理
下面描述一階邏輯的公理。如上所述，一個給定的一階理論有進一步的非邏輯公理。下列邏輯公理刻畫了本文的樣例一階邏輯的一種演算。
對於任何理論，知道公理的集合是否可用算法生成，或是否存在算法確定合式公式為公理，是很有價值的。
如果存在生成所有公理的算法，則公理的集合被稱為遞歸可枚舉的。
如果存在算法在有限步驟後確定一個公式是否是公理，則公理的集合被稱為遞歸的或“可判定的”。在這種情況下，你還可以構造一個算法來生成所有的公理：這個算法簡單的（隨著長度增長）一個接一個的生成所有可能的公式，而算法對每個公式確定它是否是個公理。
一階邏輯的公理總是可判定的。但是在一階理論中非邏輯公式就不必需如此。
1.量詞公理
下列四個公理是斷言演算的特徵：
1. PRED-1:
，
2. PRED-2:
，
3. PRED-3:
，
4. PRED-4:
。
它們實際上是公理模式：表達式
表示對於其中任何
不是自由的；而表達式
表示對於任何
帶有額外的約定，即
表示把 中的所有
替代為項
的結果。
2.等式和它的公理
在一階邏輯中對使用等式（或恆等式）有多種不同的約定。本節總結其中主要的。不同的約定對同樣的工作給出本質上相同的結果，區別主要在術語上。
1.對等式的最常見的約定是把等號包括為基本邏輯符號，並向一階邏輯增加等式的公理。等式公理是
1)
2) 對於任何函式
，
；
3）對於任何關係P（包括 = 自身），
2.其次常見的約定是把等號包括為理論的關係之一，並向這個理論的公理增加等式的公理。在實際中這是同前面約定最難分辨的，除了在沒有等式概念的不常見情況下。公理是一樣的，唯一的區別是把它叫做邏輯公理還是這個理論的公理。
3.在沒有函式和有有限數目個關係的理論中，有可能以關係的方式定義等式，通過定義兩個項s和t是相等的，如果任何關係通過把s改變為t在任何討論下都沒有改變。例如，在帶有一個關係∈的集合論中，我們可以定義
為
的縮寫。這個等式定義接著自動的滿足了關於等式的公理。
4.在某些理論中有可能給出特別的等式定義。例如，在帶有一個關係 ≤的偏序的理論中，我們可以定義
為
的縮寫。
一階邏輯的元邏輯定理
下面列出了一些重要的元邏輯定理。
3. 一元斷言邏輯（就是說，斷言只有一個參數的斷言邏輯）是可判定的。
