所謂一階(形式)語言，就是用狹義謂詞演算範圍內的邏輯概念所表達的語言，具體地說，就是用個體變元、個體常元、函式符號、關係符號或稱謂詞符號（一般包括等號在內），以及與、或、非、蘊涵等命題連線詞，還有“存在一個體”和“對一切個體”兩種量詞所表達的語言。其特點是，量詞“存在”、“對一切”只允許對個體使用，不允許對集合或謂詞等使用。它不包括“存在（個體集合的）一個子集”這樣的量詞。一階模型論的語言是一階語言。在一階語言中，由任一組命題所成的集合T稱為一個形式理論。如果有一個數學結構M，當用其中的概念解釋T的命題中諸符號後，能使T的每一命題都在M中成立，則稱M是T的一個模型。一階邏輯的模型論是模型論的基礎，事實上，任何一種邏輯系統都有各自的模型論。除各種邏輯的模型論外，模型論的新發展層出不窮：用模型論手法來研究邏輯系統也叫做模型論邏輯；用模型論方法比較各種邏輯系統的強弱，分析各種邏輯系統的特點，叫抽象邏輯的模型論；用遞歸論方法研究模型論問題產生遞歸模型論；只研究有限模型的構造和判定叫有限模型論；用模型論的思想去研究代數結構、群、環、模、域等叫做代數模型論；研究模型分類的理論叫穩定性理論。現代模型論對計算機科學也有一定影響。
基本介紹
- 中文名：一階形式語言
- 外文名：first order language
- 別稱：一階語言
- 所屬學科：數學
- 相關概念：一階邏輯，一階算術等
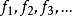
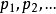
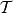
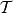
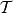
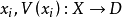
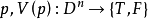
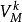
基本介紹,相關概念,
基本介紹
一階形式語言由以下部分構成。
(1)字元表
個體變元：
，或者
。
常元：
。
函式符號：
。
謂詞符號：
。
特殊謂詞符號：=。
邏輯聯結詞：
。
量詞：
。
括弧：(，)。
(2)形成規則
①項的形成規則：
(i) 任一個體變元
，任一常項變元c都是一個項。
(ii) 若
是一個帶k個自變元的函詞，
是項，則
是一個項。
(iii)只有由定義(i)~(ii)歸納定義得到的字元串是項。
②公式的形成規則：
(i)若是一個帶k個自變元的函詞，
是項，則
是一個公式。
(ii)若p是一個帶k個自變元的謂詞，是項，則
是一個公式。
(iii)若A，B是公式，則
是公式。
(iv)若A是公式，是一個變元，則
是公式。
(v)只有由(i)~(iv)歸納定義得到的字元串是公式。
(3)語句形成規則
如果公式A不含任何自由變元，則是A語句。上述結構構成一階語言。
(4)給定一階語言
，
是一個一階理論，如果它包括：
①謂詞演算的所有公理；
②一個中語句組成的集合，有窮或者無窮，它們構成非邏輯公理；
③謂詞演算的所有推理規則。
(5)中的一個語句A是理論的一個定理，如果A是(4)中的①或②語句，或者是以邏輯公理或非邏輯公理為前提，使用的推理規則得到的語句。
(6)中的一個結構(或稱模型)M由一個論域D及一階公式的變元的解釋V所組成的非空集合構成，記作
：
對於項
；
對於函詞
；
對於謂詞
，用
或
表示V的某一次(個)映射，如
表示V的第k次(個)映射使p為假。
一階形式語言的研究有時被稱為一階邏輯，或者初等邏輯。它構成現代邏輯的大部分內容。但是，現代邏輯的奠基者如弗雷格、皮亞諾以及懷特海和羅素等人都提出過高階語言的問題。
高階邏輯比一階邏輯有更強的表達力。一階邏輯的“局限性定理”表明一階語言在表達資源上的限制。諸如有限性、可數性和良基性等許多中心數學概念都不能在任何一個一階語言中得到表達，自然數集、實數域以及歐幾里得空間等結構也都不能得到充分的描述。這些局限性定理沒有一個適用於高階語言，而且上述概念和結構也都有二階刻畫。二階和高階語言因此也有很強的表達力，幾乎和非形式的數學語言一樣強。結果，它們更難以研究，也更難以駕馭。
一階形式語言是目前套用最普遍的邏輯語言。但是，一階形式語言的語法生成能力有一定的局限性。它沒有部分量詞。在改進後即增加部分量詞符號和量詞運算功能後，它可以方便地表示亞里士多德三段論的改進形式：擴展的三段論(如果認為亞里士多德三段論包括部分量詞命題的話，也需要一階形式語言的改進)。
相關概念
一階形式語言相關重要概念定義如下：
一階命題變元的解釋是對(項或謂詞或函詞)變元的一個賦值(實例化)。
有量詞約束的公式稱為量化公式。
對一個量化公式
(或
)，稱其子公式A是量詞
(或
)的轄域。
在公式A中，一個變項
如果出現在某個形如(或)的量詞的轄域中，或它就緊跟在∀(或∃)後面，則稱在A中的這處出現是約束的。變項的非約束的出現，稱為自由出現。
如果
在A中有一處自由出現，則稱
是A中的自由變項。如果在A中的所有出現都是約束的，則是A中的約束變項。
