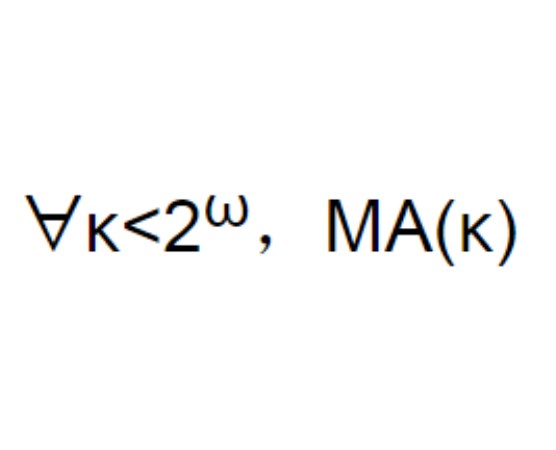馬丁公理

馬丁公理(Martin axiom)簡稱MA，是集合論的一條假設，它有多種等價的形式。馬丁公理是1970年由馬丁等人提出來的，它與ZFC的其他公理完全不同，不象一個“真”的公理，但是由它可以推出數學上重要的結果。馬丁公理是連續統假設的推論，因此可以看成是弱連續統假設。馬丁公理在數學上有一系列的重要套用。特別重要的是，舍拉在1974年證明懷特海猜想在ZFC下是不可判定的。同樣，許多拓撲學問題也有類似情況。

基本介紹

• 中文名：馬丁公理
• 外文名：Martin axiom
• 簡稱：MA
• 所屬學科：數學（集合論）
• 簡介：獨立於ZFC公理系統的著名假設
• 提出者：馬丁(D.A.Martin)等人

基本介紹

馬丁公理(Martin axiom)簡稱MA，是獨立於ZFC公理系統的著名假設之一，是近代數學基礎理論的重要論題。設κ為任意基數，令MA(κ)表示下列命題：對任何滿足可數鏈條件的偏序集〈P，≤〉及由P的稠密子集組成的基數不大於κ的集簇G，存在P中的濾子G，使得對任何D∈G，G交D不空，即G∩D≠∅，MA(2^ω)為假，對任何κ′<κ，MA(κ)→MA(κ′)，MA(ω)成立，因此MA(κ)→κ<2^ω。馬丁公理為：ᗄκ<2^ω，MA(κ)，記為MA。

相關介紹及結論

馬丁公理由美國學者馬丁(D.A.Martin)與羅伯托姆(F.Rowbottom)於1970年左右提出，以色列學者索洛韋(R.M.Solovay)與特納鮑姆(S.Tennenbaum)於1971年利用疊代力迫法證明若ZF系統相容，則ZFC+MA+2^ω>ω₁也相容，從而得出MA+ᒣCH與ZFC系統相容，另一方面，若ZF系統相容，則ZFC+ᒣMA也相容，因此MA相容且獨立於ZFC系統，由於CH→MA，因此MA也獨立於CH，美國數學家科恩(P.J.Cohen)已經證明連續統假設在ZFC公理系統中不可證，法國數學家、工程師萊維(A.Lévy)與索洛韋證明即使假設可測基數存在，也不能得出CH為真，因此，許多集合論學家覺得連續統假設在“現實世界”中“不大可能”為真。然而，連續統假設有許多推論很符合人們的直觀，它還可以使許多概念或運算得以簡化，設計馬丁公理的初衷在於減弱連續統假設的結論，使得某些由連續統假設得出的結論在減弱的假設下仍然成立。馬丁與索洛韋於1970年證明下列連續統假設下成立的重要結論在馬丁公理下仍然成立：對任何基數κ<2^ω，由馬丁公理可以得出：

1.2^κ=2^ω；

2.每個基數為κ的幾乎分離簇A⊂P(ω)不可能為最大幾乎分離簇；

3.κ個實直線R上的勒貝格測度為0的子集的並的勒貝格測度仍為0；

4.實直線R上的κ個第一範疇子集的並仍為R上的第一範疇子集。

由上列結論可以看出，馬丁公理並不是簡單地否定在ω與2^ω之間不存在基數，而是斷言，若在此間存在基數，這些基數具有類似於ω的一些性質。事實上，有許多能由CH解決的傳統數學問題也可以用MA解決，由於MA獨立於CH，因此同樣也有一些CH下為真的命題在MA+ᒣCH下為假。

馬丁公理除了偏序形式的定義之外，還有一些其他的等價表述形式，這些表述形式體現出馬丁公理可以用於多種不同的數學領域中，如馬丁公理的拓撲形式可簡單地表述為：若X為任何具有可數鏈條件的豪斯多夫空間，則X不能表示為小於2^ω個X的無處稠密子集的並，馬丁公理的布爾代數形式可表述為：若B為一個具有可數鏈條件的完備布爾代數，T為基數小於的B的一個稠子集簇，則在B^ω上存在T超濾子。

馬丁公理與ZF系統的公理不同，它不具備直覺上的自明性，因此，它實質上不是公理而是一 種集合論假設，然而，馬丁公理在現代數學基礎理論中占有相當重要的地位，它有大量的推論，其中有一些已經成為打開許多數學難題的鑰匙，馬丁公理還可以作為證明或發現某些相容或獨立於ZFC系統的命題的一種工具，由於MA與ZF(C)系統相容，假如利用MA證明某命題Φ為真，則Φ與ZF(C)系統相容，從而ᒣΦ在ZF(C)系統中不可證，有時能通過檢查MA→Φ的證明過程消去MA的使用，從而得出Φ為ZF(C)系統的定理，或者發現Φ在ZF(C)系統中也不可證，從而得出Φ獨立於ZF(C)系統，例如，著名的蘇斯林假設的相容性問題就是藉助馬丁公理才得以解決的。索洛韋等人1971年證明MA+ᒣCH→SH，由於MA+ᒣCH相容，因此SH相容;美國學者傑希(T.J.Jech)等人也已證明ᒣSH相容，故SH獨立於ZFC系統.對馬丁公理的研究主要集中於下列兩個方面：一方面減弱或加強馬丁公理的條件或結論，以尋求馬丁公理更廣泛的套用，如對偏序加適當限制等；另一方面對有關馬丁公理的更大量的研究是馬丁公理的套用研究，目前馬丁公理已被套用到無窮組合論、模型論、拓撲學、測度論、函式論及代數學等眾多數學領域，對馬丁公理的研究已經成為許多學科中的獨立研究分支。