基本介紹
概念
問題的提出
問題已有的解決
廣義連續統假設


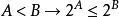




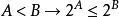

1874年格奧爾格·康托爾猜測在可列集基數和實數基數之間沒有別的基數,這就是著名的連續統假設。它又被稱為希爾伯特第一問題,在1900年第二屆國際數學家大會上,...
《集合論和連續統假設》(Set Theory and the Continuum Hypothesis)美國邏輯學家柯亨(P.J. Cohen,1934—)著。1966年發表。全書共4章。以1965年春在哈佛大學授課...
連續統是一個數學概念。當人們籠統地說:“在實數集裡實數可以連續變動”,也就可以說實數集是個連續統;更嚴格的描述需要使用序理論、拓撲學等數學工具。這裡的連續...
在數學上,連續統這一術語至少有兩種精確定義,但並不等價。另外,連續統一詞有時即指實數線或者實數集,這是較舊的叫法;見連續統假設。...
蘇斯林假設(Suslin hypothesis)簡稱SH.獨立於ZF公理系統的著名假設之一。...下面是蘇斯林假設與馬丁公理、連續統假設、可構造性公理之間關係的一些主要研究...
1963年,美國數學家科恩(P.Choen)證明連續統假設與ZF公理彼此獨立。因而,連續統假設不能用ZF公理加以證明。在這個意義下,問題已獲解決。...
1963年,美國數學家科亨證明連續假設和策梅洛--弗倫克爾集合論公理是彼此獨立的。因此,連續統假設不能在策梅洛--弗倫克爾公理體系內證明其正確性與否。希爾伯特第1...
連續統假設與廣義連續統假設是否成立?如果成立,如何證明,這曾是集合論中的一個大問題。希爾伯特在1900年的國際數學家大會上提出的23個未解決的數學問題,作為今後...
廣義連續統假設,就是對所有無窮基數 ,都不存在界乎 與 之間的基數。參考資料 1. 李娜.基於哲學邏輯的集合論研究:浙江大學學報(人文社會科學版),2017 ...
連續統假設在ZFC公理系統中不可證,法國數學家、工程師萊維(A.Lévy)與索洛韋證明即使假設可測基數存在,也不能得出CH為真,因此,許多集合論學家覺得連續統假設在...
哥德爾證明選擇公理和連續統假設協調性的方法是定義一種類型的集合,叫做可構成集。假如把集合論中集合的概念完全用可構成集合的概念來理解,那么集合論中的一些概念...
不過,康托爾的集合論並不是完美無缺的,一方面,康托爾對“連續統假設”和“良序性定理”始終束手無策;另一方面,19和20世紀之交發現的布拉利-福蒂悖論、康托爾...
任何一種科學理論在未得到實驗確證之前表現為假設學說或假說。 有的假設還沒有...黎曼猜想連續統假設 化學 阿伏伽德羅定律 病理學 各種致病原因的假說 地理學...
不過康托爾的集合論並不是完美無缺的,一方面,康托爾對“連續統假設”和“良序性定理”始終束手無策;另一方面,19和20世紀之交發現的布拉利-福蒂悖論、康托爾...
P.J.科恩(P.Choen),數學家。生於美國,是波蘭猶太移民的後裔,1966年獲獎,他證明了連續統假設與ZF集合公理系統彼此獨立,從而使連續統假設成為一種既不能證明,又...
選擇公理和其逆命題都被證明和集合論的策墨羅-弗蘭克公理相容;同樣的結果對於連續統假設也成立。這些結果是公理化集合論的一部分,而那是模型論的一個特定套用。...
也就是說,連續統假設成立與否無法由ZFC確定。 第二題 算術公理之相容性 已解決 庫爾特·哥德爾在1930年證明了哥德爾不完備定理。 第三題 兩四面體有相同體積之...
3年以後又證明了(廣義)連續統假設的相容性定理,並於1940年發表。他的工作對公理集合論有重要影響,而且直接導致了集合和序數上的遞歸論的產生。此外,哥德爾還從事...
1.G.康托爾的連續統假設問題;1963年,P.J.科恩證明了:連續統假設的真偽不可能在策梅洛-弗倫克爾公理系統內判明。希爾伯特 2. 算術公理的相容性;1931年,K....
更甚之,利用力迫法的技巧,可以證明連續統假設獨立於策梅羅-弗蘭克爾公理之外。因此,即使是這種極一般的公理也還不能被視為是數學的決定性基礎。...
任何數學命題都應有客觀的真假標準.雖然連續統假設和選擇公理已被證明對於ZF系統具有獨立性,它們仍然應有真假之分.現代數學柏拉圖主義反對用各種人為標準取代數學真理...
奇異基數假設比廣義連續統假設弱。但和廣義連續統假設一樣,奇異基數假設探討連續統函式的取值,並猜測它總是取到最小的可能值。現代集合論的研究表明,在某種大基數...
6.馬丁公理.馬丁公理(MA)的研究,源出於給連續統假設一個較弱的形式.連續統假設(CH)斷言,在。與2‘之間不存在基數,而馬丁公理斷言,若-I CH成立,則任何小於2...
