阿列夫

阿列夫是集合論的一個特定符號，表示無窮基數的一個希伯來文字母，讀為阿列夫(aleph) 。習慣上習慣把阿列夫作為無窮基數的代名詞。

基本介紹

• 中文名：阿列夫 
• 外文名：aleph
• 適用範圍：數理科學

簡介

阿列夫是集合論的一個特定符號，表示無窮基數的一個希伯來文字母，讀為阿列夫(aleph) 。

性質

習慣上習慣把阿列夫作為無窮基數的代名詞， 可以看成一個定義域為序數列 ord，陪域為無窮基數類的雙射類函式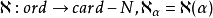： 滿足下列條件：

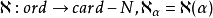
1、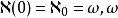 是自然數集的基數；

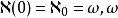
2、對任何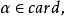

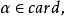
3、若β 是極限基數，則

其中，α⁺ 是α 的後繼序數， 是 的後記基數。

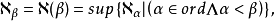
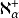
套用

類函式確定了無窮基數的正則序列，每一個無窮基數必恰是某一個 ， 是後繼基數的充分必要是 α 是後繼序數；是極限基數的充分必要條件是 α 是極限序數。當人們把看成基數為的所有序數中之最小者時，就是一個序數。它的型用 ω_α 表示。因此， 在序列中的位置，該型序列時序數序列的子序列。