基本介紹
- 中文名:劉維爾數
- 外文名:Liouville number
- 領域:數學
定義



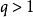
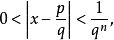

基本性質

劉維爾常數




超越性
概述

證明







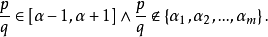

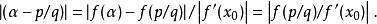




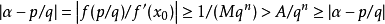







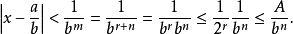



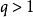
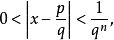














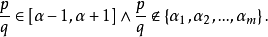

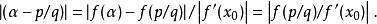




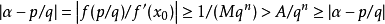







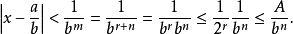
超越數的存在是由法國數學家劉維爾(Joseph Liouville,1809—1882)在1844年最早證明的。關於超越數的存在,劉維爾寫出了下面這樣一個常數:a=0.1...
劉維爾(Joseph Liouville) 法國數學家,一生從事數學、力學和天文學的研究,涉足廣泛,成果豐富,尤其對雙周期橢圓函式、微分方程邊值問題和數論中的超越數問題有深入...
這是第一個獲證的超越數,而非故意構造的(比較劉維爾數);由夏爾·埃爾米特(Charles Hermite)於1873年證明。其實,超越數主要只有自然常數(e)和圓周率(π)。自然...
劉維爾成功地證明了這個數是一個超越數。在“劉維爾數”構造出來之後二十多年,數學家康托證明了:所有代數數的集合是可數的,即代數數的個數與自然數一樣多!在...
≈ 1.30357 7269 康威常數 ≈ 2.68545 20010 辛欽常數 劉維爾常數 = 0.12345678910111213141516… 錢珀瑙恩數 ≈ 0. 00787 49969 9 蔡廷常數 常數...
在這裡,λ(n)是劉維爾函式莫比烏斯函式是一個數論函式,它同時也是一個積性函式(i.e.μ(ab) =μ(a)μ(b), a,b互質)當n不等於1時,n所有因子的莫比烏斯...
超越數的存在是由法國數學家劉維爾(Joseph Liouville,1809—1882)在1844年最早證明的。關於超越數的存在,劉維爾寫出了下面這樣一個無限小數:a=0.1...
劉維爾(Joseph Liouville) 法國數學家,一生從事數學、力學和天文學的研究,涉足廣泛,成果豐富,尤其對雙周期橢圓函式、微分方程邊值問題和數論中的超越數問題有深入...
λ(n) -劉維爾函式,關於能整除n的質因子的數目γ(n),定義為γ(n)=(-1)...2. 算數函式 - 維基百科 .維基百科.2011-12-20[引用日期2012-08-09]V...
4.劉維爾函式λ(n)的逆λ-1(n)=μ(n)λ(n)。5.設g(n)=λ*U= ,則 [1] 參考資料 1. 《數學辭海》編輯委員會.數學辭海·第一卷.北京:中國科學...
最有名的狄利克雷級數要數黎曼ζ函式了,即數列an恆等於 1 時的情形。...更廣泛的性質如下:對於一個劉維爾函式, ,有:另外一個例子是關於拉馬努賈函式...
