幾何三大問題

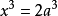
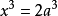
幾何三大問題（Three major geometric problems）是指二千四百多年前，古希臘幾何學家提出的尺規作圖問題（ruler-and-compass construction），即只使用圓規和直尺，並且只準許使用有限次，來解決不同的平面幾何作圖題。幾何三大問題即為三等分角問題、化圓為方問題和倍立方問題。

基本介紹

• 中文名：幾何三大問題
• 外文名：Three major geometric problems
• 別稱：尺規作圖問題
• 內容：三等分角、化圓為方、倍立方問題

簡介

幾何三大問題(Three major geometric problems)，亦稱尺規作圖問題，源於古希臘是幾何學中的著名問題，主要包括尺規作圖三大問題：

（1）三等分角問題：即把任意一個已知角三等分；

（2）立方倍積問題：即求作一個立方體，使它的體積等於已知立方體的體積的2倍；

（3）化圓為方問題：也稱圓積問題，即求作一個正方形，使它的面積等於一個已知圓的面積。

這三個問題吸引了歷代許多學者進行研究，長期未能解決，被稱為幾何三大問題。直至1837年，Wantzel用代數方法首先證明了（1）、（2）兩個問題均屬尺規作圖不能問題。1882年，林德曼(Lindemann)證明了第三個問題也屬於尺規作圖不能問題.1895年，克萊因(Klein, (C. )F.)總結了前人的研究，著有《幾何三大問題》一書，給出三大問題不可能用尺規來作圖的簡明證法，徹底解決了兩千多年的懸案。如果不限制作圖工具，幾何三大問題根本就不是什麼難題，而且早已解決。公元前5世紀，雅典的智人學派以上述三大問題為中心開展研究，正因為問題不能用尺規來解決，常常使人進人新的領域中去，促進了數學的發展.如激發了圓錐曲線、割圓曲線以及三、四次代數曲線的出現。

內容

三等分角問題

三等分角問題的完整敘述為：在只用圓規及一把沒有刻度的直尺將一個給定角三等分。在尺規作圖（指用沒有刻度的直尺和圓規作圖）的前提下，此題無解。若將條件放寬，例如允許使用有刻度的直尺，或者可以配合其他曲線使用，可以將一給定角分為三等分。

立方倍積問題

立方倍積問題(problem of duplication of a cube)亦稱倍立方體問題、德里安問題、Delos問題、德洛斯問題 、第羅斯問題等，是幾何三大問題之一。假設已知立方體的棱長為，所求立方體的棱長為，則，令，有。可以證明，若此方程有有理根，不外乎±1，±2，但它們都不是方程的根，因而不存在有理根，根據“有理係數的三次方程若無有理根，則長度等於它的任何實根的線段不能僅用尺規作圖”的定理，立方倍積屬尺規作圖不能問題。

化圓為方問題

化圓為方問題（problem of quadrature of circle），也稱圓積問題，由古希臘著名學者阿納克薩戈勒斯提出的，但是阿納克薩戈勒斯一生也未能解決自己提出的問題。該問題為求作一個正方形，使其面積等於已知圓的面積，其難度在於作圖使用工具的限制。若不受標尺的限制，化圓為方問題並非難事，歐洲文藝復興時代的大師，義大利數學家達文西（1452－1519）用已知圓為底，圓半徑的為高的圓柱，在平面上滾動一周，所得的矩形，其面積恰為圓的面積，所得矩形的面積為，，然後再將矩形化為等積的正方形即可。

意義

雖然三大幾何作圖難題都被證明是不可能由尺規作圖的方式做到的，但是為了解決這些問題，數學家們進行了前赴後繼的探索，最後得到了不少新的成果，發現了許多新的方法。同時，它反映了數學作為一門科學，它是一片浩瀚深邃的海洋，仍有許多未知的謎底等待這我們去發現。