古希臘幾何作圖的三大問題是:①
化圓為方,求作一正方形,使其面積等於一已知圓;②三等分任意角;③倍立方,求作一立方體,使其體積是一已知立方體的兩倍。這些問題的難處,是作圖只許用直尺(沒有刻度,只能作直線的尺)和圓規。經過兩千多年的探索,最後才證明在尺規的限制下,根本不可能作出所要求的圖形。
希臘人強調作圖只能用直尺圓規,有下列原因:
①希臘幾何的基本精神,是從極少的基本假定(定義、公理、公設)出發,推導出儘可能多的命題。對於作圖工具,自然也相應地限制到不能再少的程度。
②受柏拉圖哲學思想的影響。柏拉圖片面強調數學在訓練智力方面的作用而忽視其實用價值。他主張通過幾何學習達到訓練邏輯思維的目的,因此工具要有所限制,正象體育競賽要有器械的限制一樣。
③以畢達哥拉斯學派為代表的希臘人認為圓是最完美的平面圖形,圓和直線是幾何學最基本的研究對象。有了尺規,圓和直線已經能夠作出,因此就規定只使用這兩種工具。歷史上最早明確提出尺規限制的是伊諾皮迪斯,以後逐漸成為一種公約,最後總結在歐幾里得的《
幾何原本》之中。
圓和正方形都是常見的圖形,怎樣用尺規作一個正方形與已知圓等積?在歷史上,也許沒有任何一個幾何問題象這個"化圓為方"問題那樣強烈地引起人們的興趣。早在公元前5世紀就有許多人研究這個問題,希臘人對於這種活動用一個專門的字"
"來表示,意思是“獻身於化圓為方問題”,可見事情相當普遍。這問題的最早研究者是安納薩戈拉斯,他因"不敬神"的罪名被捕入獄,在獄中潛心研究化圓為方問題。以後著名的研究者有希波克拉底、安提豐、希皮亞斯等人。安提豐提出一種“窮竭法”,是近代極限論的雛形。先作圓內接正方形(或正6邊形),然後每次將邊數加倍,得內接8、16、32、…邊形,他相信“最後”的正多邊形必與圓周重合。這樣就可以化圓為方了。結論是錯誤的,然而卻提供了求圓面積的近似方法,成為阿基米德計算
圓周率方法的先導。與中國
劉徽的
割圓術不謀而合。
用尺規二等分一個角是輕而易舉的,對於某些角,如90°、135°、180°,三等分也不難。自然會提出三等分任意角的問題。如能將60°角三等分,就可以作出正18邊形和正9邊形,三等分角問題就是由這一類問題引起的。關於倍立方問題的起源,有兩個神話傳說。第一個說鼠疫襲擊提洛島(愛琴海上小島),一個預言者說已經得到神的諭示,必須將立方形的阿波羅祭壇體積加倍,瘟疫方能停息。
 希臘幾何三大問題
希臘幾何三大問題一個工匠簡單地將壇的各邊加倍(體積變成原來的8倍),這並不符合神的意旨,因此瘟疫更加猖獗。錯誤發現後,希臘人將這個”提洛問題”去請教柏拉圖。柏拉圖說:神的真正意圖是想使希臘人為忽視幾何學而感到羞愧。另一個故事說克里特王米諾斯為兒子修墳,命令將原來設計的體積加倍,但仍保持立方的形狀。
公元前5世紀,雅典的“智人學派”以上述三大問題為中心,開展研究。正因為不能用尺規來解決,常常使人闖入新的領域中去。例如激發了圓錐曲線、割圓曲線以及三、四次代數曲數的發現。
17世紀解析幾何建立以後,尺規作圖的可能性才有了準則。1837年P.L.旺策爾給出三等分任意角和倍立方不可能用尺規作圖的證明,1882年C.L.F.von林德曼證明了 π的超越性,化圓為方的不可能性也得以確立。1895年(C.)F.克萊因總結了前人的研究,著《幾何三大問題》(中譯本,1930)一書,給出三大問題不可能用尺規來作圖的簡明證法,徹底解決了兩千多年的懸案。
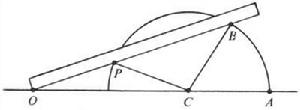
雖然如此,還是有許多人不管這些證明,想壓倒前人所有的工作。他們宣稱自己已解決了三大問題中的某一個,實際上他們並不了解所設的條件和不可解的道理。三大問題不能解決,關鍵在工具的限制,如果不限工具,那就根本不是什麼難題,而且早已解決。例如阿基米德就曾用巧妙的方法三等分任意角。下面為了敘述簡單,將原題稍加修改。在直尺邊緣上添加一點,命尺端為。設所要三等分的角是∠,以為心,為半徑作半圓交角邊於、;使點在延線上移動,點在圓周上移動,當尺通過時,聯(見圖)。由於==,易知。
 希臘幾何三大問題
希臘幾何三大問題這裡使用的工具已不限於尺規,而且作圖方法也與公設不合。另外兩個問題也可以用別的工具解決。
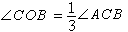 希臘幾何三大問題
希臘幾何三大問題 希臘幾何三大問題
希臘幾何三大問題 希臘幾何三大問題
希臘幾何三大問題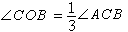 希臘幾何三大問題
希臘幾何三大問題