基本介紹
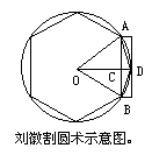 劉徽割圓術示意圖片.
劉徽割圓術示意圖片.割圓術(cyclotomic method)
所謂“割圓術”,是用圓內接
正多邊形的面積去無限逼近圓面積並以此求取
圓周率的方法。
“圜,一中同長也”。意思是說:圓只有一個中心,圓周上每一點到中心的距離相等。早在我國先秦時期,《墨經》上就已經給出了圓的這個定義,而公元前11世紀,我國西周時期數學家
商高也曾與
周公討論過圓與方的關係。認識了圓,人們也就開始了有關於圓的種種計算,特別是計算圓的面積。我國古代數學經典《
九章算術》在第一章“
方田”章中寫到“半周半徑相乘得積步”,也就是我們現在所熟悉的公式。
為了證明這個公式,我國魏晉時期數學家
劉徽於公元263年撰寫《
九章算術注》,在這一公式後面寫了一篇1800餘字的註記,這篇註記就是數學史上著名的“割圓術”。
數學意義
“割圓術”,則是以“圓內接正多邊形的面積”,來無限逼近“圓面積”。劉徽形容他的“割圓術”說:割之彌細,所失彌少,割之又割,以至於不可割,則與圓合體,而無所失矣。
即通過圓內接
正多邊形細割圓,並使正多邊形的
周長無限接近圓的周長,進而來求得較為精確的圓周率。
劉徽發明“割圓術”是為求“圓周率”。那么圓周率究竟是指什麼呢?它其實就是指“圓周長與該圓直徑的比率”。很幸運,這是個不變的“
常數”!我們人類藉助它可以進行關於圓和球體的各種計算。如果沒有它,那么我們對圓和球體等將束手無策。同樣,圓周率數值的“
準確性”,也直接關乎到我們有關計算的準確性和精確度。這就是人類為什麼要求圓周率,而且要求得準的原因。
根據“圓周長/圓直徑=圓周率”,那么圓周長=圓直徑*圓周率=2*半徑*圓周率(這就是我們熟悉的圓周長=2πr的來由)。因此“圓周長公式”根本就不用背的,只要有國小知識,知道“圓周率的含義”,就可自行推導計算。也許大家都知道“圓周率和π”,但它的“含義及作用”往往被忽略,這也就是割圓術的意義所在。
由於“圓周率=圓周長/圓直徑”,其中“直徑”是直的,好測量;難計算精確的是“圓周長”。而通過劉徽的“割圓術”,這個難題解決了。只要認真、耐心地精算出圓周長,就可得出較為精確的“圓周率”了。——眾所周知,在中國祖沖之最終完成了這個工作。
發展歷史
中國古代從先秦時期開始,一直是取“
周三徑一”(即圓周
周長與直徑的比率為三比一)的數值來進行有關圓的計算。但用這個數值進行計算的結果,往往誤差很大。正如劉徽所說,用“周三徑一”計算出來的
圓周長,實際上不是圓的周長而是
圓內接正六邊形的周長,其數值要比實際的圓周長小得多。東漢的
張衡不滿足於這個結果,他從研究圓與它的外切
正方形的關係著手得到圓周率。這個數值比“周三徑一”要好些,但劉徽認為其計算出來的圓周長必然要大於實際的圓周長,也不精確。劉徽以
極限思想為指導,提出用“割圓術”來求圓周率,既大膽創新,又嚴密論證,從而為圓周率的計算指出了一條科學的道路。
在劉徽看來,既然用“
周三徑一”計算出來的圓周長實際上是
圓內接正六邊形的周長,與圓周長相差很多;那么我們可以在圓內接正六邊形把圓周等分為六條弧的基礎上,再繼續等分,把每段弧再分割為二,做出一個圓內接正十二邊形,這個正十二邊形的周長不就要比正六邊形的周長更接近圓周了嗎?如果把圓周再繼續分割,做成一個圓內接正二十四邊形,那么這個正二十四邊形的周長必然又比正十二邊形的周長更接近圓周。這就表明,越是把
圓周分割得細,誤差就越少,其內接正多邊形的周長就越是接近圓周。如此不斷地分割下去,一直到圓周無法再分割為止,也就是到了圓內接正多邊形的邊數無限多的時候,它的周長就與圓周“合體”而完全一致了。
按照這樣的思路,劉徽把圓內接正多邊形的面積一直算到了正3072邊形,並由此而求得了圓周率 為
3.1415和 3.1416這兩個近似數值。這個結果是當時世界上圓周率計算的最精確的數據。劉徽對自己創造的這個“割圓術”新方法非常自信,把它推廣到有關圓形計算的各個方面,從而使漢代以來的數學發展大大向前推進了一步。以後到了南北朝時期,
祖沖之在劉徽的這一基礎上繼續努力,終於使圓周率精確到了
小數點以後的第七位。在西方,這個成績是由法國數學家
韋達於1593年取得的,比祖沖之要晚了一千一百多年。祖沖之還求得了圓周率的兩個
分數值,一個是“
約率” ,另一個是“
密率”.,其中 這個值,在西方是由德國的奧托和荷蘭的安東尼茲在16世紀末才得到的,都比祖沖之晚了一千一百年。劉徽所創立的“割圓術”新方法對中國
古代數學發展的重大貢獻,歷史是永遠不會忘記的。
基本算法
根據劉徽的記載,在劉徽之前,人們求證
圓面積公式時,是用圓內接正十二邊形的面積來代替圓面積。套用
出入相補原理,將圓內接正十二邊形拼補成一個長方形,借用長方形的面積公式來論證《九章算術》的圓面積公式。劉徽指出,這個長方形是以
圓內接正六邊形周長的一半作為長,以圓半徑作為高的長方形,它的面積是圓內接正十二邊形的面積。這種論證“合徑率一而弧周率三也”,即後來常說的“
周三徑一”,當然不嚴密。他認為,圓內接
正多邊形的面積與圓面積都有一個差,用有限次數的分割、拼補,是無法證明《九章算術》的圓面積公式的。因此劉徽大膽地將極限思想和無窮小分割引入了
數學證明。他從圓內接正六邊形開始割圓,“割之彌細,所失彌少,割之又割,以至不可割,則與圓周合體,而無所失矣。”也就是說將圓內接正多邊形的邊數不斷加倍,則它們與圓面積的差就越來越小,而當邊數不能再加的時候,圓內接正多邊形的面積的
極限就是圓面積。劉徽考察了內接多邊形的面積,也就是它的“冪”,同時提出了“差冪”的概念。“差冪” 是後一次與前一次割圓的差值,可以用圖中陰影部分三角形的面積來表示。同時,它與兩個小黃三角形的面積和相等。劉徽指出,在用圓內接
正多邊形逼近圓面積的過程中,圓半徑在正多邊形與圓之間有一段余徑。以余徑乘正多邊形的邊長,即2倍的“差冪”,加到這個正多邊形上,其面積則大於圓面積。這是圓面積的一個
上界序列。劉徽認為,當圓內接正多邊形與圓是合體的極限狀態時,“則表無餘徑。表無餘徑,則冪不外出矣。”就是說,余徑消失了,余徑的長方形也就不存在了。因而,圓面積的這個上界序列的極限也是圓面積。於是內外兩側序列都趨向於同一數值,即,圓面積。
利用圓內接或
外切正多邊形,求圓周率近似值的方法,其原理是當正多邊形的邊數增加時,它的邊長和逐漸逼近圓周。早在公元前5世紀,古希臘學者
安蒂豐為了研究
化圓為方問題就設計一種方法:先作一個圓內接
正四邊形,以此為基礎作一個圓內接
正八邊形,再逐次加倍其邊數,得到正16邊形、正32邊形等等,直至正多邊形的邊長小到恰與它們各自所在的圓周部分重合,他認為就可以完成化圓為方問題。到公元前3世紀,古希臘科學家
阿基米德在《論球和圓柱》一書中利用
窮竭法建立起這樣的命題:只要邊數足夠多,圓外切正多邊形的面積與內接正多邊形的面積之差可以任意小。阿基米德又在《圓的度量》一書中利用正多邊形割圓的方法得到圓周率的值小於三又七分之一而大於三又七十分之十 ,還說
圓面積與外切
正方形面積之比為11:14,即取圓周率等於22/7。公元263年,中國數學家劉徽在《
九章算術注》中提出“割圓”之說,他從
圓內接正六邊形開始,每次把邊數加倍,直至圓內接正96邊形,算得圓周率為3.14或157/50,後人稱之為
徽率。書中還記載了圓周率更精確的值3927/1250(等於3.1416)。劉徽斷言“割之彌細,所失彌少,割之又割,以至於不可割,則與圓合體,而無所失矣”。其思想與古希臘
窮竭法不謀而合。割圓術在圓周率計算史上曾長期使用。1610年德國數學家
柯倫用2^62邊形將圓周率計算到小數點後35位。1630年
格林貝爾格利用改進的方法計算到小數點後39位,成為割圓術計算圓周率的最好結果。分析方法發明後逐漸取代了割圓術,但割圓術作為計算圓周率最早的
科學方法一直為人們所稱道。
 圓周率的三角函式算法
圓周率的三角函式算法π=lim(n→∞)1/2*sin(360°/n)*n
思想價值
在證明這個圓面積公式的時候有兩個重要思想,一個就是我們現在所講的極限思想。那么第二步,更關鍵的一步,他把與
圓周合體的這個
正多邊形,就是不可再割的這個正多邊形,進行無窮小分割,再分割成無窮多個以圓心為頂點,以多邊形每邊為底的無窮多個小等腰三角形,這個底乘半徑為小三角形面積的兩倍,把所有這些底乘半徑加起來,應該是
圓面積的兩倍。那么就等於圓周長乘半徑等於兩個圓面積。所以一個圓面積等於半周乘半徑,所以劉徽說故半周乘半徑而為
圓冪。那么他的原話就是“以一面乘半徑,觚而裁之,每輒自倍。故以半周乘半徑而為圓冪”。最後完全證明了圓面積公式, 證明了圓面積公式,也就證明了“周三徑一”的不精確。隨著圓面積公式的證明,劉徽也創造出了求圓周率精確近似值的科學程式。在劉徽之前
古希臘數學家阿基米德也曾研究過求解圓周率的問題。
劉徽所處的時代是社會上
軍閥割據,特別當時是魏、蜀、吳三國割據,那么在這個時候中國的社會、政治、經濟發生了極大的變化,特別是思想界,文人學士們互相進行辯難,所以當時成為辯難之風,一幫文人學士找到一塊,就像我們大專辯論會那樣,一個正方一個反方,提出一個命題來大家互相辯論,在辯論的時候人們就要研究討論關於辯論的技術,思維的規律,所以在這一段人們的思想解放,應該說是在春秋戰國之後沒有過的,這時人們對思維規律研究特別發達,有人認為這時人們的抽象思維能力遠遠超過春秋戰國。 劉徽在《九章算術注》的自序中表明,把探究數學的根源,作為自己從事數學研究的最高任務。他注《九章算術》的宗旨就是“析理以辭,解體用圖”。“析理”就是當時學者們互相辯難的代名詞。劉徽通過析數學之理,建立了中國傳統數學的理論體系。眾所周知,古希臘數學取得了非常高的成就,建立了嚴密的演繹體系。然而,劉徽的 “割圓術”卻在人類歷史上首次將
極限和無窮小分割引入
數學證明,成為人類文明史中不朽的篇章。
 劉徽割圓術示意圖片.
劉徽割圓術示意圖片. 圓周率的三角函式算法
圓周率的三角函式算法
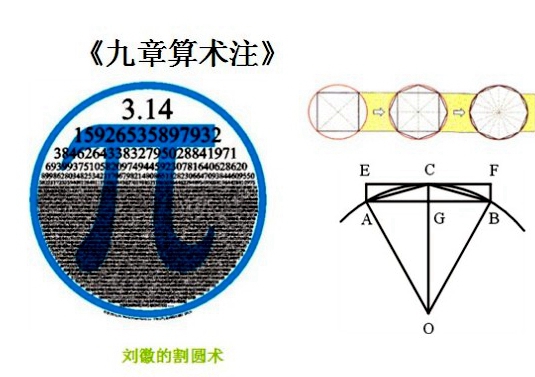
 劉徽割圓術示意圖片.
劉徽割圓術示意圖片. 圓周率的三角函式算法
圓周率的三角函式算法
