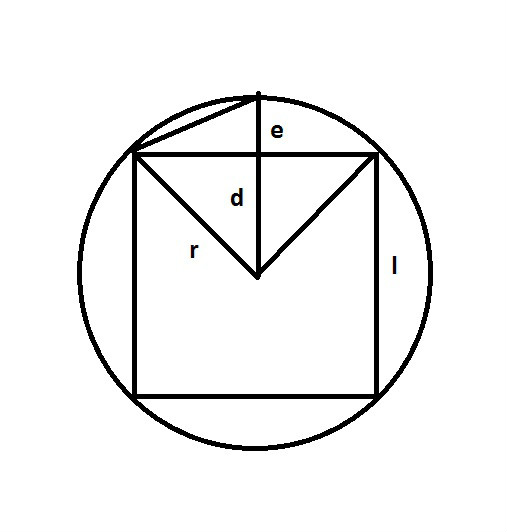
趙友欽割圓術

趙友欽割圓術是元代數學家趙友欽在所著的《革象新書》卷五《乾象周髀》篇研究的割圓術。與劉徽從內接正六角形開始不同，趙氏割圓術從分割內接正方形開始。

如圖，圓的半徑為r; 內接正方形的邊長為 ,由圓心到正方形一邊倒垂直距離為 d

d 的延長線與圓周相交點將圓周等分為正八邊形。

令正八邊形的邊長為k

設 l(3)為分割圓成正16邊形之邊長，趙友欽正確地推斷l(3)與l(2)的疊代關係

推廣之：

如令r=1

.....................................

圓周率

趙友欽指出，分割越細，正多邊形的邊數愈多，正多邊形越接近圓周。

角數愈多而為方者不複方漸變為圓矣。故自一二次求之至十二次精密已極

他最後將千寸直徑的圓周分割為正16384邊形，從而獲得

三尺一寸四分一厘五毫九絲二忽然有奇

基本介紹