過任意在圓O外的一點P引一條直線L1與一條過圓心的直線L2，L1與圓交於A、B（可重合，即切線），L2與圓交於C、D。則PA·PB=PC·PD。若圓半徑為r，則PC·PD=(PO-r)·(PO+r)=PO^2-r^2=|PO^2-r^2| （要加絕對值，原因見下）為定值。這個值稱為點P到圓O的冪。（事實上所有的過P點與圓相交的直線都滿足這個值）
基本介紹
- 中文名：圓冪
- 外文名：Power of a Point
- 表達式：|OP^2-R^2|
- 套用學科：數學
- 適用領域範圍：平面幾何
定義,由來,
定義
假設平面上有一圓O，其半徑為R，有一點P在圓O外，過P任作一直線與⊙O交於點A、B，PA與PB的乘積即為P到⊙O的冪，數值為OP^2-R^2。
若P點在圓內，則圓冪為R^2-OP^2；綜上所述，圓冪為|OP^2-R^2|。
符號：圓內的點的冪為負數，圓外的點的冪為正數，圓上的點的冪為零。
由來
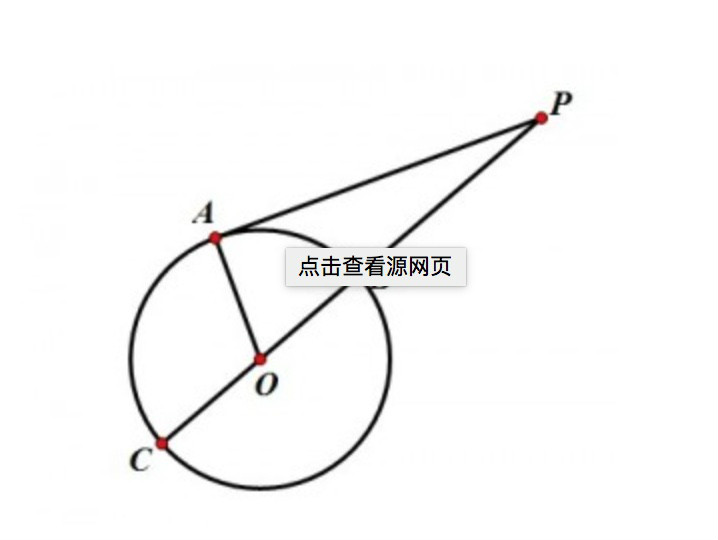
過任意在圓O外的一點P引一條直線L1與一條過圓心的直線L2，L1與圓交於A、B（可重合，即切線），L2與圓交於C、D。則PA·PB=PC·PD。若圓半徑為r，則PC·PD=(PO-r)·(PO+r)=PO^2-r^2=|PO^2-r^2| （要加絕對值，原因見下）為定值。這個值稱為點P到圓O的冪。（事實上所有的過P點與圓相交的直線都滿足這個值）
若點P在圓內，類似可得定值為r^2-PO^2=|PO^2-r^2|
故平面上任意一點對於圓的冪為這個點到圓心的距離與圓的半徑的平方差，而過這一點引任意直線交圓於A、B，那么PA·PB等於圓冪的絕對值。
