基本介紹
- 中文名:根軸
- 外文名:radical axis
- 表達式:(x-a1)^2+(y-b1)^2-(r1)^2=0(1)
- 套用學科:數學
- 適用領域範圍:物理
定義
根軸方程
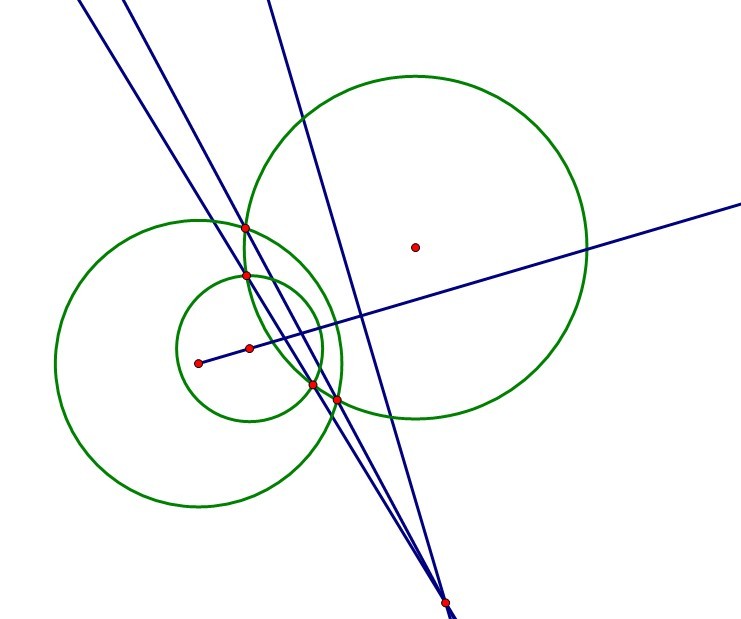
 圖1.
圖1.尺規作圖
 內含時的尺規作圖
內含時的尺規作圖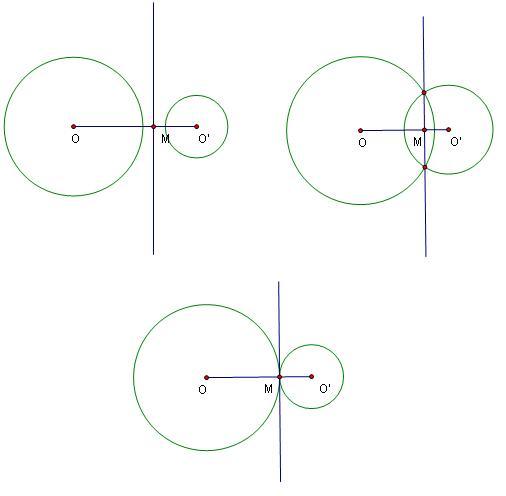
 圖1.
圖1. 內含時的尺規作圖
內含時的尺規作圖在平面上任給兩不同心的圓,則對兩圓圓冪相等的點的集合是一條直線,這條線稱為這兩個圓的根軸。另一角度也可以稱兩不同心圓的等冪點的軌跡為根軸,或者稱作...
依生長的形式形成兩種不同的根系。軸根系(直根系)、鬚根系。...... 軸根軸根 編輯 軸根(圖1) 軸根系(直根系):由胚根發育延長成主根,再由主根分枝生出許多支...
呈長方形,長與寬之比為3∶2:3。自上而下由橙、白、綠三個相等的橫長方形組成,白色長方形中心繪有24根軸條的藍色法輪。...
《後漢書·宋弘傳論》:“夫器博者無近用,道長者其功遠,蓋志士仁人所為根心者也。”明 張居正 《兩宮尊號議》:“臣仰見我皇上,大孝根心,純切懇至,臣連...
軸荷重是指機車車輛在靜止狀態時,每個輪對作用於鋼軌的質量。在設計機車時,要根據機車的總體布置,進行質量分配計算,以使最終獲得各根軸的軸重相等。機車車輛的軸...
一個動點到兩個圓的冪相等,那么這動點的軌跡是一條直線,就是這個圓的根軸.2.一個動點到兩個定點的距離的平方和等於定值,那么這個動點的軌跡是一個圓....
每台轉向架可裝2~4根軸,一般裝2~3根軸。轉向架各軸通常均為動軸,電力傳動機車的動軸幾乎都是單獨驅動的,只有單牽引電動機車轉向架和液力傳動機車轉向架的動...
共軸圓束(coaxial pencil of circles)亦稱共軸圓系。平面幾何術語。指具有某種共性的圓的集合。即平面上具有同一等冪軸的所有圓的集合。共同的等冪軸稱為共軸圓...
按天球上的小圓弧逼近衛星視軌跡實現跟蹤照相的儀器。有四根轉軸:Ⅰ軸是垂直軸;Ⅱ軸是水平軸;Ⅲ軸指向逼近視軌跡的小圓弧的極點,稱為軌道極軸;Ⅳ軸按小圓弧的...
漢語二字詞語,本義為繞某箇中心或某根軸作曲線運動。...... 漢語二字詞語,本義為繞某箇中心或某根軸作曲線運動。中文名 運轉 外文名 revolve 拼音 1、yùn...
根軸:對於兩已知圓等冪的點的軌跡是一條直線,這條直線叫兩圓的根軸。根心:圓心不共線的三個圓兩兩的根軸交於一點,這點稱為三圓的根心。垂心組:以三點...
SOHC(Single Overhead Camshaft)的中文含義是“單頂置凸輪軸”,與DOHC(Double OverheadCamshaft)相對單頂置凸輪軸在氣缸蓋上用一根凸根軸,直接驅動進、排氣門,它...
速度測量是工控系統中最基本的需求之一,最常用的是用數字脈衝測量某根軸的轉速,再根據機械比、直徑換算成線速度。脈衝測速最典型的方法有測頻率(M法)和測周期(T...
蒙日定理,指的是由加斯帕爾·蒙日提出的一個幾何定理,也叫做根心定理。指的是平面上任意三個圓,若這三個圓圓心不共線,則三條根軸相交於一點,這個點叫它們的...
