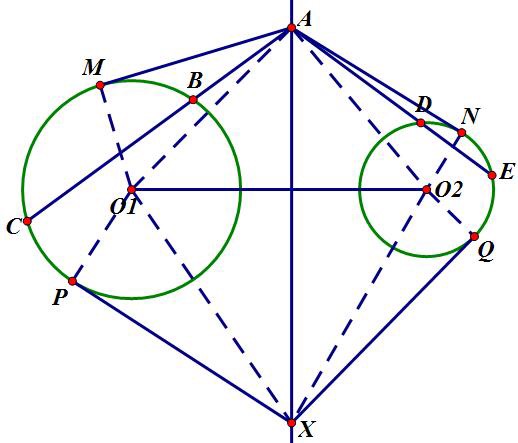
定差冪線定理:若直線l⊥線段AB於H,M1與M為l上兩點,則AM1^2一AM^2 =BM1^2 一BM^2。
推論Ⅰ(定差冪線軌跡定理)已知兩點A和B ,則滿足AM^2一BM^2=k^2(k為常數)的點M的軌跡是垂直於AB的一條直線。
推論Ⅱ(斯坦納定理)已知△ABC,由點A B 、C 分別向三邊BC、CA、AB所引的垂線共點的充要條件是:
A1B^2 一BC1^2 + C1A^2 一AB1^2 + B1C^2 一CA1^2 = 0
推論Ⅲ 給定△ABC,P是任意一點,m、n、l各是AP、BP、CP的等角線,則m、n、l三線共點或互相平行。
基本介紹
- 中文名:定差冪線定理
- 充要條件:AP ^2一AM^2 =BP^2 一BM^2
- 重要知識:點對圓的冪
- 根心:三個圓兩兩的根軸交於一點
定差冪線定理,其他重要知識,推論Ⅰ,推論Ⅱ,推論Ⅲ,定差冪線定理的證明,證法一,證法二,
定差冪線定理
概念:
定差冪線定理:PM⊥AB的充要條件是:AP ^2一AM^2 =BP^2 一BM^2。
其他重要知識
點對圓的冪:從一點A作一圓周的任一割線,從A起到和圓周相交為止的兩線段之積,稱為點A對此圓的冪。
根軸:對於兩已知圓等冪的點的軌跡是一條直線,這條直線叫兩圓的根軸。
根心:圓心不共線的三個圓兩兩的根軸交於一點,這點稱為三圓的根心。
垂心組:以三點為三角形的頂點,另一點為該三角形的垂心的四點稱為垂心組。
線段調和分割:若同一直線上四點G、A、H、B滿足 GA×HB = GB×AH,則稱它們為調和分割(harmonic division)。
完全四邊形:兩兩相交又無三線共點的四條直線及它們的六個交點所構成的圖形稱為完全四邊形。 三角形等角共軛點:與三角形的邊所成的角對應相等的一對點。
餘弦定理(廣勾股定理):在任一三角形中,
(1)銳角對邊的平方,等於兩夾邊之平方和,減去某夾邊和另一夾邊在此邊上的投影乘積的兩倍.
(2)鈍角對邊的平方,等於兩夾邊的平方和,加上某夾邊與另一夾邊在此邊延長上的投影乘積的兩倍.
調和四邊形:對邊乘積相等的圓內接四邊形。
九點圓:三角形三條高的垂足,三條邊的中點,垂心與頂點連線的中點共九點共圓。
戴維斯定理:三角形每邊所在直線上有一對點,若每兩對點共圓,則三對點都在一個圓上。
推論Ⅰ
(定差冪線軌跡定理)已知兩點A和B ,則滿足AM^2一BM^2=k^2(k為常數)的點P的軌跡是垂直於AB的一條直線。
推論Ⅱ
(斯坦納定理)已知△ABC,由點A B 、C 分別向三邊BC、CA、AB所引的垂線共點的充要條件是:
A1B^2 一BC1^2 + C1A^2 一AB1^2 + B1C^2 一CA1^2 = 0
推論Ⅲ
給定△ABC,P是任意一點,m、n、l各是AP、BP、CP的等角線,則m、n、l三線共點或互相平行。
定差冪線定理的證明
證法一
若PM⊥AB,則有AP ^2一AM^2 =BP^2 一BM^2。
證明:若直線PM⊥AB於N,則
AP^2 一AN^2 = PN^2;
AM^2 一AN^2 = MN^2.
以上兩式相減得
AP^2 一AM^2 = PN^2 一MN^2.①
同理,
BP^2 一BM^2 = PN^2 一MN^2.②
由式①、②得
AP^2 一AM^2 = BP^2 一BM^2 .③
證畢。
反之,若有AP ^2一AM^2 =BP^2 一BM^2成立,則PM⊥AB。
證明:設∠ANP=α,則∠BNP=π—α.
故AP^2 一AM^2
= AN^2 + PN^2 — 2AN·PNcosα+2AN·MNcosα一AN^2 一MN^2
= PN^2 一MN^2 一2AN·PNcosα+2AN·MNcosα.
BP^2 一BM^2
= PN^2 + BN^2 一2PN·BNcos(π—α) 一MN^2 一BN^2 + 2MN·BNcos(π—α).
= PN^2 一MN^2 + 2PN·BNcosα一2MN·BNcosα.
由式③得
2AN·MNcosα一2AN·PNcosα
= 2PN·BNcosα一2MN·BNcosα,
即MN(AN + BN)cosα
= PN(AN + BN)cosα.
從而,(PN 一MN) cosα=0,即PM cosα=0.
因此,cosα=0.
又因為0<α<π,所以α= π/2.
故PM⊥AB.
證法二
證明:以長度為d的線段AB上任意一點為原點O,過O點且垂直於線段AB的直線OM為y軸建立以OA為x正半軸的平面直角坐標系,並設A(一t,0)、B(d-t,0)、M(x,y),(其中t>0),則
∵AM^2 一MB^2=k(定值)
∴[(x+t)^2-y^2]- [(x-d+t)^2-y^2]=k
∴x=﹙d^2-2dt+k﹚/d(常數)
所以,點M的軌跡是一條垂直於AB的直線。