共軸圓束(coaxial pencil of circles)亦稱共軸圓系。平面幾何術語。指具有某種共性的圓的集合。即平面上具有同一等冪軸的所有圓的集合。共同的等冪軸稱為共軸圓束的等冪軸(或根軸)。
基本介紹
- 中文名:共軸圓束
- 外文名:coaxial pencil of circles
- 領域:數學
- 學科:幾何學
- 別稱:共軸圓系
- 定義:某種共性的圓的集合
概念,平面幾何,圓束,幾何學,
概念
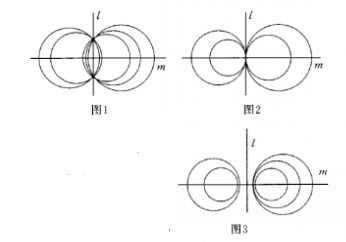
共軸圓束(coaxial pencil of circles)亦稱共軸圓系。平面幾何術語。指具有某種共性的圓的集合。即平面上具有同一等冪軸的所有圓的集合。共同的等冪軸稱為共軸圓束的等冪軸(或根軸),如圖中的直線l。共軸圓束中任意選取n個圓稱為共軸圓或稱這n個圓共軸。共軸圓束的所有圓心在同一直線上,該直線稱為圓束的圓心軸,如圖中的直線m。共軸圓束是最常討論的圓束,因此,也常把它簡稱圓束。若圓束的一圓與等冪軸有兩個公共點,則該圓束中所有圓都通過這兩個公共點。這樣的圓束稱為橢圓型圓束(如圖中圖1所示)。若圓束中的一圓與等冪軸相切,則該圓束中的所有圓都彼此相切於同一點。這樣的圓束稱為拋物型圓束(如圖中圖2所示)。若圓束中的一圓與等冪軸無公共點,則該圓束中的所有圓都與等冪軸無公共點,且各圓間也無公共點。這樣的圓束稱為雙曲型圓束(如圖中圖3所示)。
平面幾何
幾何學的基礎學科,研究平面圖形的性質的幾何學。公元前約三百年,古希臘數學家歐幾里得(Euclid)系統總結和研究了前人的幾何知識,寫成一本科學偉著《幾何原本》。書中從少數定義和公理出發,通過邏輯推理,得到一系列的定理,建立了較嚴密的幾何演繹體系,使幾何成為一門獨立學科,即歐幾里得幾何學。《幾何原本》對幾何學以後的發展和數學教育的發展都起了重要作用,它曾在西方近兩千年的時間裡,作為學校最主要的教科書,流傳於世。
古希臘的數學分為四大科:算術、幾何、天文、音樂,直到中世紀,古羅馬帝國還以古希臘的學校為模式,建立了包括初等、中等、高等三類的教育系統,其中高等教育的數學教學仍分為此四科.以後,算術分為算術與代數,幾何分為三角學與幾何,在各個時期的各種幾何課本,基本上都取材於《幾何原本》,但中間曾有一度刪去了所有證明。到14—15世紀文藝復興時期,由於生產力的發展需要,學校的智育擴大到包括算術、幾何、文學、歷史、地理、機械學等十幾個學科,在幾何中又重新重視了證明,增加了計算、測量等內容。
18世紀,法國數學教師拉克魯瓦(S.F.Lacroix)編寫教科書九卷(1796—1799),其中幾何內容參考了數學家達朗貝爾(J.le R.d′Alembert)的意見,分為平面幾何與立體幾何兩部分;德國萊布尼茨(G.W.Leibniz)的學生沃爾費(C.vonWolf)編寫初等數學教材(1713),其中,幾何部分先講平面幾何,後講立體幾何。此後,西歐各國中等學校大都將幾何分為平面幾何與立體幾何講授。
19世紀中葉以後,幾何學發展出現了各種新的分支,它們都可以分別研究其平面、立體的,甚至高維空間的情況,但是,作為幾何學最基礎學科的平面幾何,從歷史發展的過程和學校教育的實際情況來看,它的內容體系仍屬於歐幾里得幾何的範圍,它所採用的研究方法仍是直接就圖形來研究其性質的綜合方法。
圓束
複平面上一類圓周的總稱。若k1和k2為給定的兩個圓,稱同時正交k1和k2的圓的全體為圓束。按照k1和k2相交、相切及相離的情形,相應的圓束分別稱為雙曲型圓束、拋物型圓束及橢圓型圓束。
幾何學
研究圖形性質的一門數學分支。
“geometry”來自拉丁文geometria,原意是土地測量。古埃及的幾何學,起源於尼羅河泛濫後對土地所進行的重新測量。古巴比倫人已經知道了一些圖形面積與體積的求法;還知道圓周長與直徑的比為定值。
古希臘的歐幾里得,把前人的幾何知識(幾何證明與抽象概念等)系統化,整理成嚴密的演繹系統,寫出了《幾何原本》。這本書問世後,幾何學在數學中曾長期占主導地位。直到17世紀初,代數學得到發展以後,幾何學在數學中所處的主導地位才被代數學取代。而用代數方法研究幾何問題,又導致了解析幾何學的產生。在18、19世紀,由於力學、工程、測量等方面的需要,產生了畫法幾何學、射影幾何學和微分幾何學。而對歐氏第五公設的研究、又導致非歐幾何學的產生。幾何學的各個分支,可以定義為研究特定圖形在特定的變換下的不變性質。
我國在很早就已出現論證幾何學的萌芽。在公元前5世紀墨子所著的《墨經》中,有豐富且嚴謹的幾何方面的論述。其中所涉及的幾何內容,與歐幾里得的《幾何原本》大致相同,而且其中的定義,與現行中學幾何教科書基本相同。此外,其中還有一系列理論性的命題,反映出墨家重視抽象性及邏輯嚴密性的新思想和新嘗試。可惜,後來未能形成為嚴密的演繹體系。
20世紀以來,由於現代物理、現代工程技術的發展,又促進了微分幾何學與計算幾何學的發展。在現代,幾何學泛指對由公理所規定性質之集合進行研究的學科。皮亞諾與希爾伯特,對歐氏幾何學的現代化起過重要的作用。
“幾何”是《幾何原本》1607年的中譯本中開始使用的譯名,它的原意指“多少”或“大小”。“幾何”是意譯,並不是音意並譯。
