伴隨圓束亦稱共軛圓束。平面幾何術語,指具有某種共性的兩個圓束,即兩個垂直相交的圓束。
基本介紹
- 中文名:伴隨圓束
- 外文名:adjoint pencil of circles
- 適用範圍:數理科學
簡介,共軸圓束,
簡介
伴隨圓束亦稱共軛圓束。平面幾何術語,指具有某種共性的兩個圓束,即兩個垂直相交的圓束。
與已知圓束垂直相交的圓有無限多個,這些圓又組成一個新的圓束,這樣的兩個圓束稱為共軛圓束。若共軛圓束之一是橢圓型的,則另一個圓束必是雙曲型的;若兩共軛圓束之一是拋物型的,則另一個圓束也是拋物型的。
 圖1.
圖1.共軸圓束
(coaxial pencil of circles)
共軸圓束亦稱共軸圓系。平面幾何術語,指具有某種共性的圓的集合,即平面上具有同一等冪軸的所有圓的集合。
共同的等冪軸稱為共軸圓束的等冪軸(或根軸),如圖中的直線 l 。共軸圓束中任意選取 n 個圓稱為共軸圓或稱這 n 個圓共軸。共軸圓束的所有圓心在同一直線上,該直線稱為圓束的圓心軸,如圖中的直線 m 。共軸圓束是最常討論的圓束,因此,也常把它簡稱圓束。
若圓束的一圓與等冪軸有兩個公共點,則該圓束中所有圓都通過這兩個公共點。這樣的圓束稱為橢圓型圓束。
若圓束中的一圓與等冪軸相切,則該圓束中的所有圓都彼此相切於同一點。這樣的圓束稱為拋物型圓束。
若圓束中的一圓與等冪軸無公共點,則該圓束中的所有圓都與等冪軸無公共點,且各圓間也無公共點。這樣的圓束稱為雙曲型圓束。
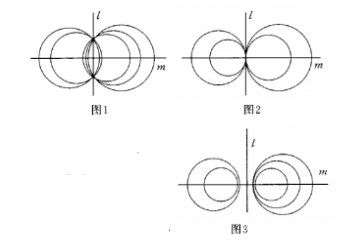 圖2.
圖2.