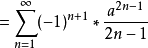基本介紹
- 中文名:割圓連比例
- 外文名:cyclotomic continued proportion
- 概述:割圓連比例是清代級數
- 歷史背景:1701年,法國耶穌會傳教
- 中心問題:已知圓弧長度,如何求弦長及矢高
- 套用學科:數學
歷史背景,連比例,明安圖連比例,二分弧,三分弧,四分弦,五分弦,十分弦,百分弧,千分弧,萬分弦,正弦展開,
歷史背景
1701年,法國耶穌會傳教士杜德美(Pierre Jartoux 1668年至1720年)來到中國,他帶來了由艾薩克·牛頓和J.格雷戈里創建的三個三角函式無窮級數



這些計算 的“捷法”只涉及乘法和加減運算,速度遠超傳統[[劉徽割圓術]]涉及的平方根計算,因而激起了中國數學家的極大興趣。然而杜德美沒有將推導這些無窮級數的方法帶來中國。明安圖懷疑西方人不願分享他們的秘密,於是他著手進行這項工作,前後歷時30年,完成了書稿《割圜密率捷法》,他在書中創建幾何模型用於獲得三角函式無窮級數,不僅推出杜德美的三個無窮級數,還發現了六個新的無窮級數。在這個過程中,他發現和套用卡塔蘭數。
的“捷法”只涉及乘法和加減運算,速度遠超傳統[[劉徽割圓術]]涉及的平方根計算,因而激起了中國數學家的極大興趣。然而杜德美沒有將推導這些無窮級數的方法帶來中國。明安圖懷疑西方人不願分享他們的秘密,於是他著手進行這項工作,前後歷時30年,完成了書稿《割圜密率捷法》,他在書中創建幾何模型用於獲得三角函式無窮級數,不僅推出杜德美的三個無窮級數,還發現了六個新的無窮級數。在這個過程中,他發現和套用卡塔蘭數。
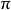
 明安圖發現卡塔蘭數 《割圜密率捷法》卷三
明安圖發現卡塔蘭數 《割圜密率捷法》卷三連比例
如圖一 ABC,BCD,CDE,DEF,FDG…… 是一系列相似三角形,於是。 連比例
連比例
 連比例
連比例AB:BC=BC:CD=CD:EF=EF:DF=DF:DG;
AB為第一率,以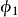 表示
表示
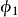
BC為第二率,以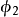 表示
表示
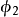
BC為第二率,以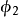 表示
表示
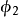
CD為第三率,以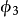 表示
表示
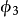
DE為第四率,以 表示
表示

EF為第五率,以 表示
表示

FG為第六率,以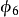 表示
表示
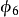
……
第m率:

於是:
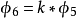
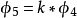
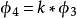
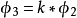

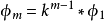

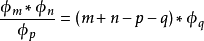
明安圖連比例
二分弧
如圖BCD為全弧,AB=AC=AD=為半徑,令半徑=1;BD為通弦,BC、CD為1/2 分弧。作BG=BC=x,作直線CG;又作DH=DC,連CH直線。因此, 割圓圓比例
割圓圓比例
 割圓圓比例
割圓圓比例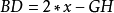
作EJ=EF,FK=FJ;延長BE直線至L,並令EL=BE;作BF=BE,使F在AE線上。連BF延長至M,並BF=MF;連LM,顯然LM通過C點。將三角形BLM以BM為軸反轉成三角形BMN,C點重合G,L點重合N。將三角形NGB以BN為軸反轉至BMI;顯然BI=BC。

作CG之平分線BM,並令BM=BC;連GM、CM;作CO=CM交BM於O;作MP=MO;作NQ=NR,R為BN與AC之交點。∠EBC=1/2 ∠CAE=1/2 ∠EAB;因此∠EBM=∠EAB;於是得到一系列相似三角形:ABE,BEF,FJK,BLM,CMO,MOP,CGH,而且三角形CMO=三角形EFJ;於是得:
*連比第一率:AB=AC=AD=AE
*連比第二率:BE=BC=BF=C
*連比第三率:EF=CM
*連比第四率:FJ
*連比第五率:JK=OP

1:BE=BE:EF;即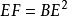
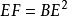

於是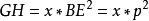 ,
,
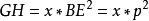
即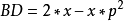
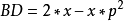
因為 風箏形ABEC 與BLIN相似,。

<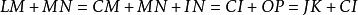
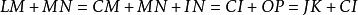
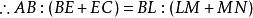
即

:令BL=q
: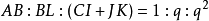
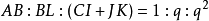
:

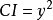
:

由此得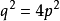 或
或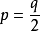
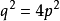
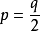
:又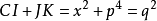 ,代人p值得:
,代人p值得:
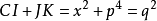
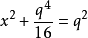
: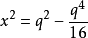
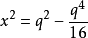
:上式平方之,兩邊除以16:
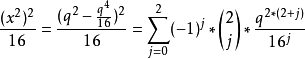
:即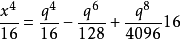
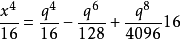
依次類推
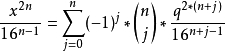
將下列二式相加,可以消去

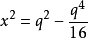

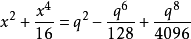
:同理
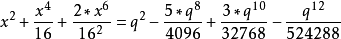
.......

展開式各項分子的係數 1,1,2,5,14,42,132……(見圖二 明安圖原圖最後一行,由右至左讀)乃是[[卡塔蘭數]],明安圖是發現此數的世界第一人<ref>羅見今 《明安圖和他的冪級數展開式》數學傳播34卷1期, pp. 65-73</ref>。
因而得到:

其中

:明安圖利用他首創的遞推關係:
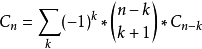

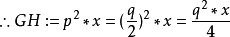
代人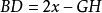
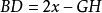
:最後得到。
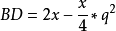
: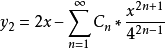
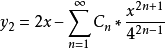
;
在圖一中令BAE角=α,BAC角=2α
- x=BC=sinα
- q=BL=2BE=4sin(α/2)
- BD=2sin(2α)
明安圖獲得的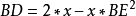
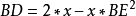
:就是正弦倍角和正弦半角度的正弦展開式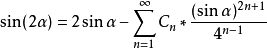
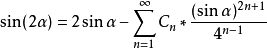
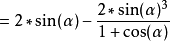


三分弧
 明安圖割圓密率三分弧
明安圖割圓密率三分弧如圖,BE為全弧通弦,BC=CE=DE=a為三等分弧。AB=AC=AD=AE=1 為半徑。連BC、CD、DE、BD、EC;作BG、EH=BC,Bδ=E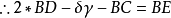 α=BD,於是三角形Cαβ=Dδγ;又三角形Cαβ與三角形BδD相似。
α=BD,於是三角形Cαβ=Dδγ;又三角形Cαβ與三角形BδD相似。
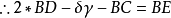
因此:


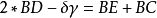
依次類推,最後得:
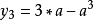
四分弦
 四分弦
四分弦
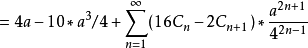
。
:幾何意義:
明安圖獲得正弦四倍角度三角展開式:

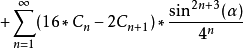
五分弦
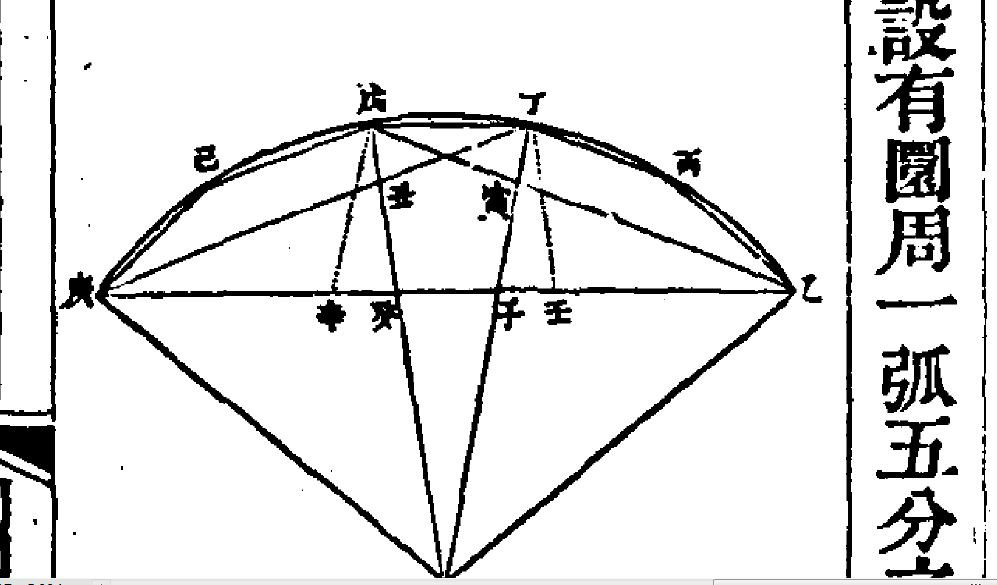 明安圖五分弦
明安圖五分弦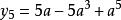
:幾何意義:

十分弦
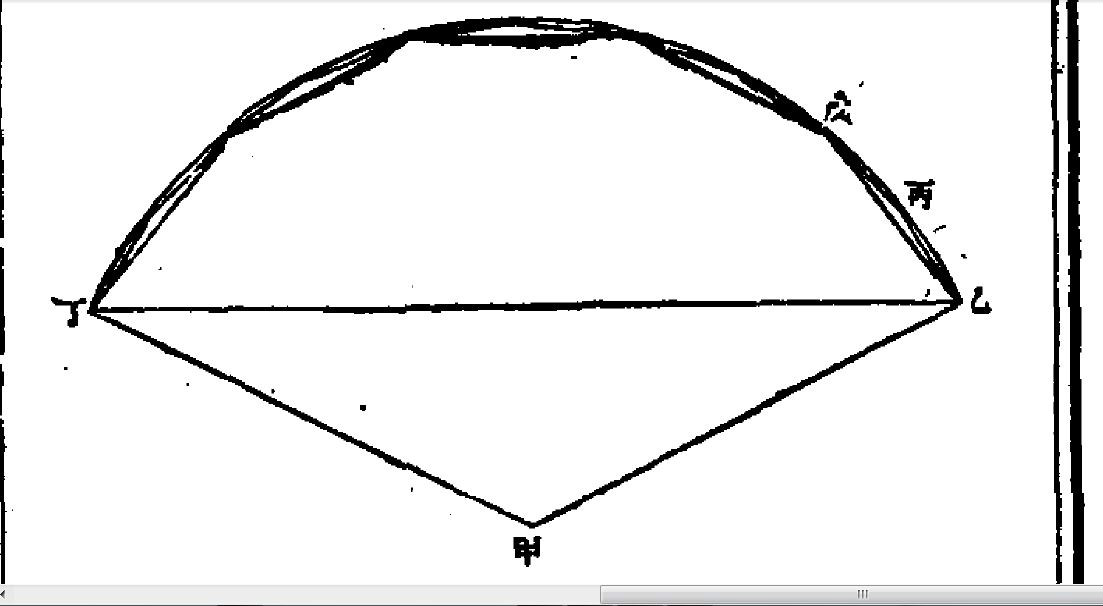 十分弦圖
十分弦圖從十分弦開始,明安圖不再作幾何模型,而是對無窮級數進行代數運算
顯然十分弦等於五分弦和二分弦的組合,即
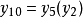

展開即得:
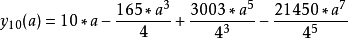
百分弧
同理:
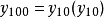
展開後即得:
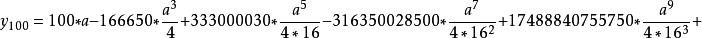
千分弧
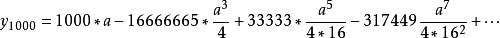
萬分弦

正弦展開

令 r=1