月形定理

月形定理(lunar theorem)是勾股定理的推廣，以直角三角形的兩直角邊為直徑分別向形外作半圓，再用直角三角形的外接(半)圓截這兩個半圓而成的兩個月形面積的和等於該直角三角形的面積。月形定理實際上是把“直角三角形斜邊上圖形的面積等於兩直角邊上相似圖形面積的和”用在半圓上，它最先是由希俄斯的希波克拉底(Hippocrates，(C))提出來的，所以也稱希波克拉底定理，他用此定理去研究化圓為方問題，由於他的疏忽，而用了不正確的推論，以致有一時期有人誤認為化圓為方的問題已經解決，實際上化圓為方是一個尺規作圖不能問題。

基本介紹

• 中文名：月形定理
• 外文名：lunar theorem
• 所屬學科：數學（平面幾何）
• 簡介：勾股定理的推廣
• 提出者：希波克拉底(Hippocrates，(C))
• 別名：希波克拉底定理

基本介紹

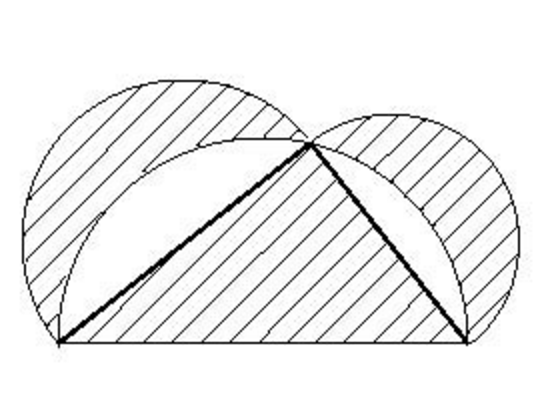
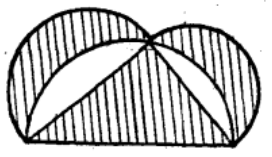定理直角三角形直角邊上兩個月形面積之和，等於直角三角形的面積(圖1)。

圖1

這個定理是希臘著名幾何學家希波克拉圖(Hippocrates)(也譯作“希波克拉底”等)提出來的。其證明並不複雜。

月形定理的證明

設直角三角形兩直角邊為a，b，斜邊為c，兩月形面積為S₁，S₂，三角形面積為S。

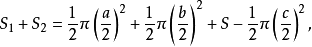
希波克拉圖在幾何學上貢獻頗大，他的《幾何綱要》是第一本幾何教科書，歐幾里德的《幾何原本》就是以它為藍本的。現在幾何中將字母注於圖形上， 如點日A，直線日AB等，相傳為希氏創始而為後世所沿用。希氏曾致力於“化圓為方”和“立方倍積”問題的研究，月形定理是其之出發點，由於他的疏忽，曾使人們一度認為化圓為方十分容易，不少人上了當。他把月形定理套用到正方形上，得出正方形邊上兩個月形面積之和等於該正方形面積之半的結論(圖2)，這顯然是正確的。既然圓的內接正方形有這樣的性質，那么圓內接正六邊形“當然”也就有類似性質：正六邊形三邊上月形面形之和等於正六邊形的面積之半。希氏沒有發現這種“想當然”的結論是不正確的，進而套用這個錯誤定理引出了更錯誤的結論：圓可以化為方！請看他的推理過程(圖3)：

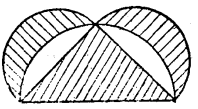圖2

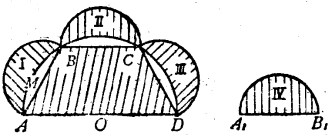圖3

設AB是圓內接正六邊形的一邊，A₁B₁=AB，直徑為AD的半圓面積，等於直徑分別為AB、BC、CD和A₁B₁的四個半圓面積之和(請讀者自己驗證)。

S_梯形ABCD= 4S_{直徑為AB的半圓}一3S_弓形AMB

= 4S_Ⅳ一3S_弓形AMB=S_Ⅳ+ 3(S_Ⅳ-S_弓形AMB)

=S_Ⅳ+ 3S_月形。

所以S_Ⅳ=S_梯形ABCD一3S_月形。

既然假定月形Ⅰ、Ⅱ、 Ⅲ，能夠化成正方形，那么半圓Ⅳ也可化成正方形，這顯然是錯誤的。

應該承認希氏解決問題的方法是有天才的。但由於命題的假設未經一般的證明，所以得出了錯誤的結論，這個實例，對我們學習數學的青年人是很有借鑑作用的。