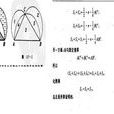
以直角三角形兩直角邊為直徑向外作兩個半圓,以斜邊為直徑向內作半圓,則三個半圓所圍成的兩個月牙面積的和等於該直角三角形的面積。這個定理叫作希波克拉底的“月牙定理”(Hippocrate's Theorem)。
希波克拉底斯(Hippocrates of Chios,古希臘人,公元前440年)希波克拉底斯,生於奇俄斯島(Chios),原以經商為業,不幸被海盜劫掠一空。為了找回被劫去的財貨,他長期住在雅典查訪,並在雅典從事幾何學的研究工作。
基本介紹
- 中文名:希波克拉蒂月牙問題
- 外文名:Hippocrate's Theorem
- 別名:希波克拉底的“月牙定理”
- 領域:國中數學
理解,推理,題1,解答,
理解
以直角三角形兩直角邊為直徑向外作兩個半圓,以斜邊為直徑向內作半圓,則三個半圓所圍成的兩個月牙(希波克拉底月牙)面積的和等於該直角三角形的面積。這個定理叫作希波克拉底的“月牙定理”(Hippocrate's Theorem)。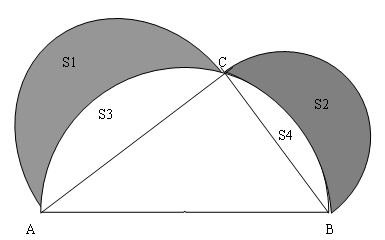

推理
題1
以AB為直徑作一半圓,取弧AB一點C,分別以AC、CB為直徑作半圓,兩個半圓與大的半圓的不重合部分即為新月
因為直徑所對圓周角為直角,三角形ABC為直角三角形, 由勾股定理AC^2+BC^2=AB^2 S(AC)=(1/2)π(AC/2)^2; S(BC)=(1/2)π(BC/2)^2; S(AB)=(1/2)π(AB/2)^2 所以S(AC)+S(BC)=S(AB) 兩邊同減去公共部分即得新月部分面積和等於直角三角形的面積 其中S(AC)表示以AC為直徑的半圓面積,依此類推例題有一個著名的希波克拉蒂月牙問題.如圖:以AB為直徑作半圓,C是圓弧上一點,(不與A、B重合),以AC、BC為直徑分別作半圓,圍成兩個月牙形1、2(陰影部分).已知直徑AC為4,直徑BC為3,直徑AB為5. (1)分別求出三個半圓的面積; (2)請你猜測:這兩個月牙形的面積與三角形ABC的面積之間有何等量關係
列式:
S兩個月牙形=(SAC-S1(三角形AC中的弓形))+(SBC-S2(三角形BC中的弓形))
=SAC+SBC-S1-S2
SABC=SAB-S1-S2
∵SAC+SBC=12.5π-SAB
∴S兩個月牙形=S三角形ABC
解答
(1)
方法:把半圓當成一個整圓算面積,然後÷2,就是半圓
SAB=πr2=π×5×5÷2=25/2π=39.25(cm2)SAC=πr2=π×3×3÷2=9/2π =14.13(cm2)
SBC=πr2=π×4×4÷2=16/2π=25.12(cm2)
(2)
∵兩個小半圓之和=14.13+25.12=39.25(cm2)
39.25(cm2)=大半圓
∴SAC+SBC=兩個小半圓之和=大半圓)
兩個小半圓之和-兩個弓形=大半圓-兩個弓形
兩個月牙=△ABC