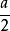立方體(幾何圖形)

立方體，也稱正方體，是由6個正方形面組成的正多面體，故又稱正六面體。它有12條邊和8個頂點。其中正方體是特殊的長方體。

基本介紹

• 中文名：立方體
• 外文名：Cube
• 別稱：正方體
• 組成：6個正方形面組成
• 引用學科：幾何學
• 含有：12條邊和8個頂點

定義

立方體，是由6個相同大小的正方形圍成的立體圖形，故又稱正六面體，英文拼寫是Cube。

立方體

立方體（Cube），是由6個正方形面組成的正多面體，故又稱正六面體（Hexahedron）、正方體或正立方體。它有12條棱（邊）和8個頂（點），是五個柏拉圖立體之一。

立方體是一種特殊的正四稜柱、長方體、三角偏方面體、菱形多面體、平行六面體，就如同正方形是特殊的矩形、菱形、平行四邊形一様。立方體具有正八面體對稱性，即考克斯特BC₃對稱性，施萊夫利符號{4,3}，考克斯特-迪肯符號，與正八面體對偶。

立方體特徵

面的圖形：正方形

面的數目：6

邊的數目：12

頂點數目：8

表面積：

體積：

二面角角度：

外接球半徑：

內接球半徑：

對偶多面體：正八面體

在所有表面積一定的長方體中，立方體的體積最大，同樣，在所有線性大小（長寬高之和）一定的長方體中，立方體的體積也是最大的。反過來，體積相等的長方體中，立方體擁有最小表面積和線性大小。

幾何性質

立方體有11種不同的展開圖，即是說，我們可以有11種不同的方法切開空心立方體的7條棱而將其展平為平面圖形，見右圖。

立方體的11種不同展開圖。

如果我們要將立方體塗色而使相鄰的面不帶有相同的顏色，則我們至少需要3種顏色（類似於四色問題）。
立方體是唯一能夠獨立密鋪三維歐幾里得空間的柏拉圖正多面體，因此立方體堆砌也是四維唯一的正堆砌（三維空間中的堆砌拓撲上等價於四維多胞體）。它又是柏拉圖立體中唯一一個有偶數邊面——正方形面的，因此，它是柏拉圖立體中獨一無二的環帶多面體（它所有相對的面關於立方體中心中心對稱）。
將立方體沿對角線切開，能得到6個全等的正4稜柱（但它不是半正的，底面棱長與側棱長之比為2:√3）將其正方形面貼到原來的立方體上，能得到菱形十二面體(Rhombic Dodecahedron)（兩兩共面三角形合成一個菱形）。

聯繫

將立方體的其中四個頂點相連，而這四個頂點任何兩條都沒有落在立方體同一條的邊上，可得到一個正四面體，其邊長為立方體邊長的，其體積為立方體體積的。

立方體的對偶多面體是正八面體。

當正八面體在立方體之內：

正八面體體積: 立方體體積=[(1/3)×高×底面積]×2: 邊=(1/3)(n/2)[(n)/2]2: n=1: 6

星形八面體的對角線可組成一個立方體。

截半立方體：從一條棱斬去另一條棱的中點得出

截角立方體

超正方體：立方體在高維度的推廣。更加一般的，立方體是一個大家族，即立方形家族（又稱超方形、正測形）的3維成員，它們都具有相似的性質（如二面角都是90°、有類似的超體積公式，即V_n-cube=a等）。

長方體、偏方面體的特例。

套用

日常生活

食鹽和糖的結晶體都是立方狀；

骰子最常見的形狀就是立方體；

1967年世界博覽會的「立方體房間」。

遊戲

索馬立方；

扭計骰；

扭扭骰；

Slothouber-Graatsma 立方：以6個1×2×2及3個單位立方組成3×3×3的立方（僅有一個解法）；

康威立方：以3個1×1×3，13個1×2×4，及1×2×2和2×2×2的長方體各一個，組成一個5×5×5的立方（572個解）。

視錯覺

奈克方塊；

不可能方塊（上方右圖）。

數學問題

體積與表面積

• 體積=長×寬×高=邊
• 表面積=每個面面積×6=邊×6

倍立方體問題

參見尺規作圖，已經證明此題無法用無刻度的直尺與圓規去畫出的位置

最大的橫切面

立方體的橫切面只有四種：

• 三角形
• 矩形
• 五邊形
• 六邊形

其中以正六邊形的面積最大,若立方體的棱長為a,則正六邊形的面積為。