所謂”展開圖“,就是將製件的表面按一定順序而連續地攤平在一個平面上所得到的圖樣。這種圖樣在造船、航空、機械、化工、電力、建築、輕紡、食品等工業部門都得至l壙泛的套用,顯然,展開圖畫得是否準確,直接關係到製件質量、生產效率、產品成本等問題。
基本介紹
- 中文名:展開圖
- 外文名:expansion dwg
- 學科:數學
- 套用:航空、機械、化工、電力等
- 目的:畫法幾何研究
展開圖介紹
基本方法
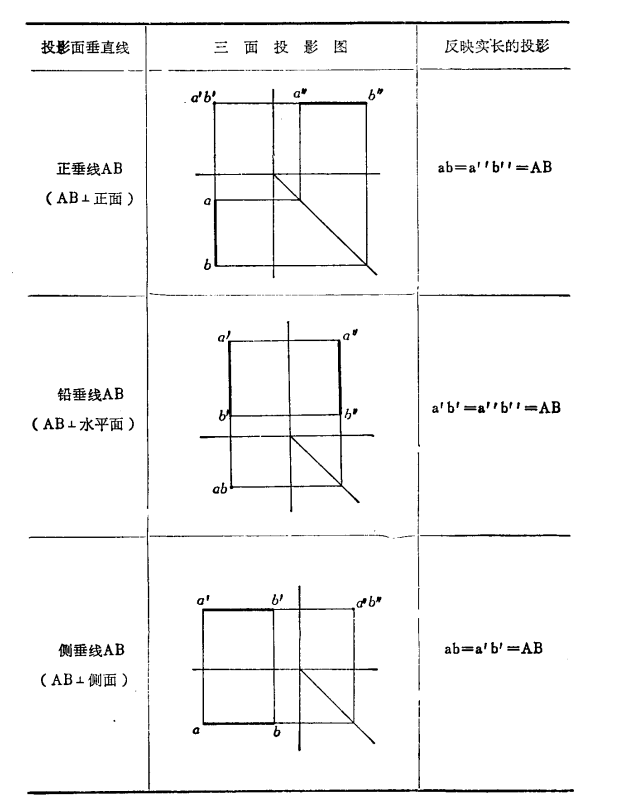
求直線段實長



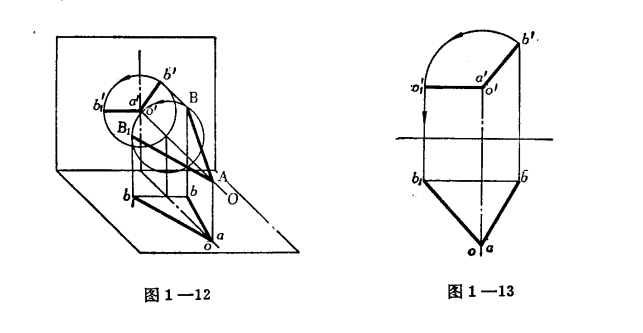
結合線的畫法

展開圖圖例
所謂”展開圖“,就是將製件的表面按一定順序而連續地攤平在一個平面上所得到的圖樣。這種圖樣在造船、航空、機械、化工、電力、建築、輕紡、食品等工業部門都得至l壙泛的套用,顯然,展開圖畫得是否準確,直接關係到製件質量、生產效率、產品成本等問題。











所謂”展開圖“,就是將製件的表面按一定順序而連續地攤平在一個平面上所得到的圖樣。這種圖樣在造船、航空、機械、化工、電力、建築、輕紡、食品等工業部門都得至...
目標展開圖是指明確目標與目標責任的圖表,是目標展開的最後一個環節,適用圖表形式將目標和實現目標的對策的等主要內容公布於眾,便於共同執行。...
平面立體展開圖(development of plane-surfacesolid)展開圖的一種.平面立體的表面為平面,展開圖由若干個多邊形(三角形、四邊形等)組成。...
表面展開指將物體表面按其實際形狀依次攤開在同一個平面上。...... 展開後所得到的圖形,稱為物體的表面展開圖,簡稱展開圖。物體表面根據其幾何性質可分為可展開面...
本書以鈑金工展開圖為核心,對現代實際生產中所接觸到的大多數鈑金製件的放樣展開圖作了認真細緻的圖示和清晰的說明。書中還對鈑金工製作工藝中的放樣、下料、剪下...
目標實施展開圖,亦稱“目標實施統籌圖”。用幾何圖形、符號、箭頭、指向線、文字描述目標、對策、主要控制點及目標實施步驟等內容的圖。目標實施展開圖形象清楚,邏輯...
《鈑金展開圖集》是2008年機械工業出版社出版的圖書。作者楊玉傑。本圖集中,作者整理了施工中經常遇到的鈑金展開圖畫法百餘例,在每個圖例中儘量用簡潔明了的圖面及...
展開的涵義:將系統的目標從上到下、層層分解落實的過程,稱為目標展開,其總的要求是:按整分合原則建立目標體系,按激勵原則落實目標責任。目標展開是目標確定過程的...
《鈑金展開放樣(圓弧伸直畫法)》是是作者在總結多年生產和教學經驗的基礎上,套用理論與實踐相結合的方法,並參考了有關資料編寫而成的。本書主要內容包括鈑金展開...
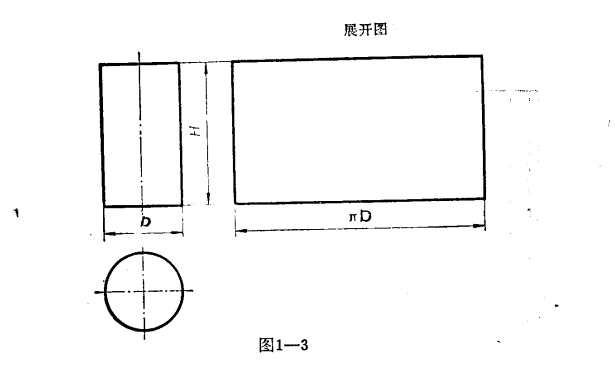
可展曲面展開圖(development of developablecurved surface)展開圖的一種.曲面上的兩條連續素線平行或相交時,該曲面稱為可展曲面,如圓柱、圓錐、切線曲面等.圖1為...
《鈑金展開圖畫法及典型實例》是2015年化學工業出版社出版的圖書,作者:孫鳳翔。...... 《鈑金展開圖畫法及典型實例》是2015年化學工業出版社出版的圖書,作者:孫鳳翔...
《鈑金展開圖畫法及套用實例》是2007年化學工業出版社出版的圖書,作者是王敏。本書講述了鈑金工識圖及繪圖的基本知識和套用實例,從製圖的基礎知識開始,以“看圖”...
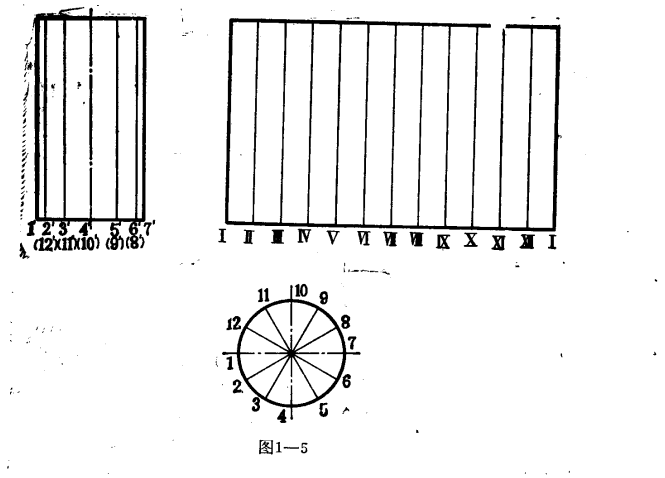
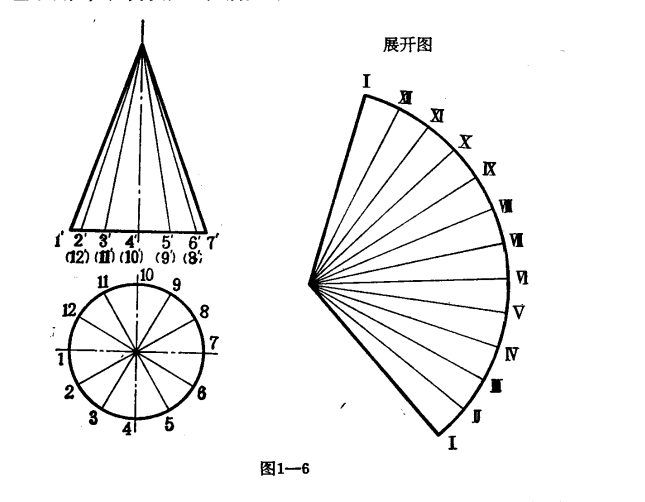
不可展曲面展開圖(non-developable curvedsurface development)展開圖的一種.曲面上的條連續素線是交叉的,或母線是曲線時,該曲面稱為不可展曲面,如圓球、螺旋面等...
《鈑金展開入門指導122例》是2011年機械工業出版社出版的圖書, 作者是徐昌明、冉瑞明。 本書主要介紹了鈑金展開理論和展開做圖的基本知識。...
《鈑金展開下料技法與實例》是2012年機械工業出版社出版的圖書,作者是姜文深。本書是專門介紹金屬板材展開下料方法的圖書。...
《鈑金展開放樣》是2012年機械工業出版社出版的一本圖書,該書作者是聶厚章。...... 圓弧伸直在展開圖上的套用,各類形體表面展開圖的圓弧伸直畫法及平面體表面展開圖...
變形接頭展開圖(transition piece develop -ment)展開圖的一種.在管路連結中,常用變形接頭來連結斷面不同的管子,為了使流體順暢通過,接頭內表面應力求光滑.圖示為上...
《鈑金展開計算法(第2版)》是編者多年從事鈑金下料計算展開工作的經驗總結。書中計算公式簡單,在第1版的基礎上,針對每一個構件提出了具體的板厚處理方法,並增加...
《常用異步電動機繞組展開圖與接線圖》是2010年金盾出版社出版的一本圖書。本書從介紹電動機繞組的基礎知識及其展開圖和接線圖的畫法人手,繪編了Y2(IP54)、Y(...
《電機繞組修理彩色圖集(展開圖·布線圖·接線圖)》是由中國水利水電出版社於2014年出版的圖書,該書由譚影航編著。...
《建築給水排水三維展開圖繪圖方法》是1999年出版的圖書,作者是鄭美文。...... 《建築給水排水三維展開圖繪圖方法》是1999年出版的圖書,作者是鄭美文。...
陳國宇等編著的《鈑金展開技術》根據職業學校焊接技術套用專業課程標準,結合我校(唐山市丰南職教中心)對焊接技術套用專業相關企業崗位技能、職業能力調查結果,由我校本...
鈑金件展開圖的作圖方法有:圖解作圖法、計算解析法以及計算機作圖法。 目前廣大中小工廠、小作坊,由於受到設備和技術水平所限,鈑金件展開仍是十分普遍和廣泛地套用...
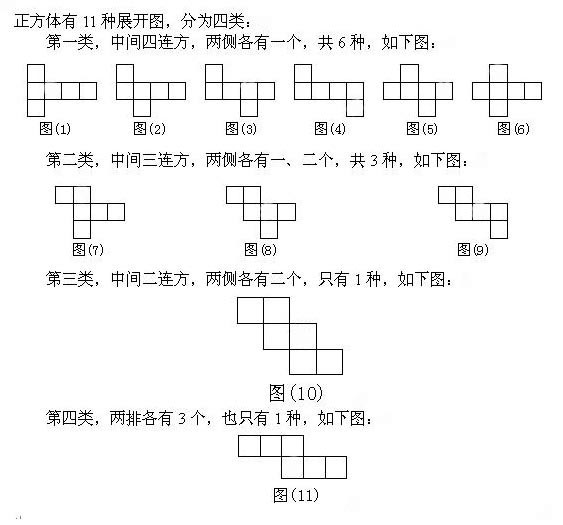
帶彩色的11種正方體展開圖 我們知道正方體有6個面,每個面都是相同的正方形.我們把6個相同的小正方形排出可能的正方體的展開圖的平面圖形.一共有35種平面圖形。...
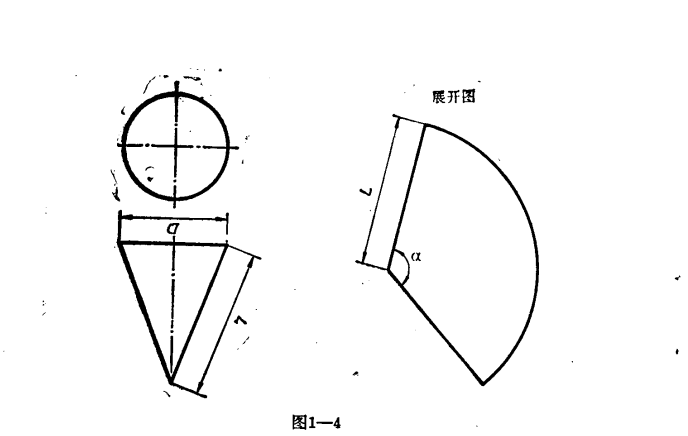
圓錐的側面積就是弧長為圓錐底面的周長×母線/2;沒展開時是一個曲面。圓錐有一個底面、一個側面、一個頂點、一條高、無數條母線,且底面展開圖為一圓形,側面...
圓錐的側面展開圖是扇形,該扇形半徑是圓錐的腰線長,弧長為底面圓周長。參考資料 1. 人民教育出版社課程教材研究所,中學數學課程教材研究開發中心.數學 必修4:人民...
