簡介
超正方體是一個有無窮多個成員的凸正
多胞形家族的四維成員,這個家族被稱為“
超方形”(或稱
立方形、
正測形),這個家族的成員與施萊夫利符號{4,3,3,……,3,3},它們都具有類似正方形和立方體的性質,如二胞角都為90°等。
超立方體這個名稱在一般的場合中特指四維的這個超正方體,不過在數學上,“超立方體”這個詞可以指n維(n>3)的任意一個
超方形,因此把它和n維的其他超方形放在一起討論時,要加“四維”以示區別。
幾何性質
在四維歐幾里得空間的標準四維方體是點(±1, ±1, ±1, ±1)的
凸包。它包含了點:
四維超立方體由八個
超平面(
)包圍。兩兩非平行超平面相交,共形成四維方體的24個正方形面。每條棱有3個立方體和3個正方形相交。在每一頂點有4個立方體、6個正方形和4條棱相交。四維方體共有8個立方體、24個正方形、32條棱和16個頂點。邊長為a的四維超正方體超體積是
,表體積是
。
 圖1.四維超立方體的展開圖
圖1.四維超立方體的展開圖若一個四維超立方體的棱長為1,則其外接超球半徑為1,外中交超球(經過超立方體各棱中點的三維超球)半徑為
,內中交超球(經過超立方體各面中心的三維超球)半徑為
,內切超球半徑為
。事實上,對於任意一個棱長為a的n維
超方形,其自身中心到任意一個k維元素的中心的距離為
。
四維方體的每一頂點與4條棱相鄰,所以四維方體的頂點形是
正四面體。所以四維方體的
施萊夫利符號是{4,3,3}。其對偶多胞體是
正十六胞體,施萊夫利符號是{3,3,4}。
投影
1.二維投影
超;立方體的構造方法可以通過以下方式來想像:
 圖2.展示如何從點開始得到超正方體的圖像
圖2.展示如何從點開始得到超正方體的圖像四維方體的結構不易想像,但可以投射至3維或2維空間。在我們將其投影到二維空間中後,把頂點位置調整,可以了解更多。如此獲得的圖像,不再反映四維方體空間構造,而是反映頂點間的聯繫。
2.三維投影
超正方體到三維空間的正對胞的
平行投影有一個
立方體凸包。最近端的和最遠端的胞被投影成了立方體凸包本身,而剩餘6個立方體胞則被投影成了立方體的6個
正方形面。
 圖3.超正方體平行投影的凸包
圖3.超正方體平行投影的凸包超正方體到三維空間的正對面的平行投影有一個
長方體(正四稜柱)凸包。2對胞被投影成了長方體凸包的上下兩半,而剩餘4個胞則投影成了正四稜柱凸包的側面。
超正方體到三維空間的正對棱的平行投影有一個
正六稜柱形的凸包。6個胞被投影成了菱形稜柱,它們在正六稜柱凸包中的排列方式就如同立方體正對頂點的平行投影中正方形面投影成的
菱形在
六邊形凸包中的排列方式。剩餘的2個胞被投影成了正六稜柱的兩個底面。
超正方體到三維空間的正對頂點的平行投影有一個
菱形十二面體凸包,事實上,我們正好有兩種方法能將菱形十二面體分割成4個全等的
平行六面體,因此菱形十二面體中總計有8個全等的平行六面體。超正方體在這種投影下胞的投影就正好是這8個平行六面體。這個投影的體積是超正方體所有投影中最大的。
套用
超級並行/分布計算機是未來一 個時期內計算機的主要發展方向,超立方體是實現其系統 內結 點互連的最具 吸引力的拓撲結構之一。針對超立方體的拓撲結構可在解決通信時間延遲,大幅度提高通信速度的通信技術。
從原理上講,在這種系統中,任兩結點間的通信速度均與結點數無關,原理結構思想是,以6維立方體為基本單元,其中的64個結點連成立方體同時又都連到匯流排上,連到任一結點的相鄰通信通道間均有旁路程控開關,以便在通信中旁路中間結點實現源結點和目的結點間的直通。
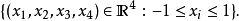
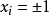

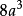
 圖1.四維超立方體的展開圖
圖1.四維超立方體的展開圖


 圖2.展示如何從點開始得到超正方體的圖像
圖2.展示如何從點開始得到超正方體的圖像
 圖3.超正方體平行投影的凸包
圖3.超正方體平行投影的凸包