基本介紹
- 中文名:正十六胞體
- 外文名:Hexadecachoron,16-cell,4-orthoplex
- 點數:8
- 線數:24
- 面數:32
- 三維胞數:16
簡介,計算,投影,施萊格爾投影,球極投影,二維線架正投影,施萊夫利符號,類比,二胞角,與正八胞體聯繫,
簡介
它的施萊夫利符號為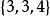 ,
,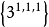 或
或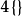 ,是超立方體的對偶。
,是超立方體的對偶。
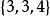
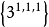
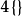
其頂點圖是正八面體,正16胞體每條棱上有4個正四面體。
另外,它有下列幾種別名:
正四面體反稜柱(Tetrahedron antiprism)、
Tetracross(四維正軸體,沒有官方中文翻譯)、
4-orthoplex(即正四面體反稜柱,orthoplex和cross都指代同一個多胞體,但意義不同)、
Demitesseract(半截超立方體,指代超立方體每個面上連線得到的東東,沒有官方中文翻譯)
計算
對於一個邊長為a的正16胞體,其超體積為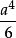 ,超表面積為
,超表面積為 ,對角線長為a。
,對角線長為a。
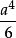

投影
施萊格爾投影
正八面體我們一定不陌生,但是看過右圖的恐怕就不多了。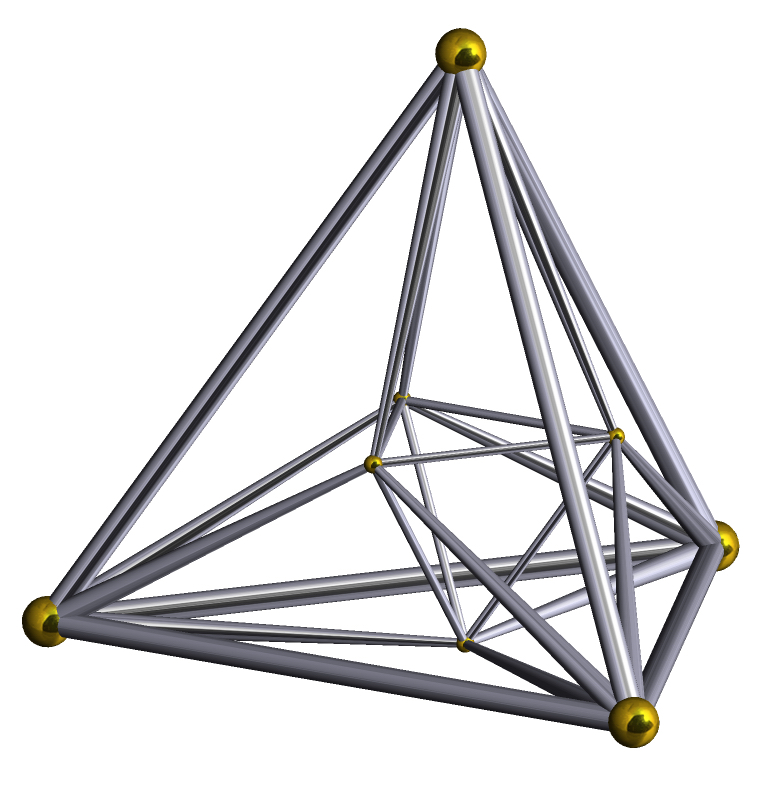

右圖是當一個人對著正八面體的一個面靠近的很近的時候會看到的——準確地說眼睛是在這個正八面體的外接球面上看到的。這就是正八面體的施萊格爾投影。
可以看到這個投影中外面是一個大正三角形,裡面是一個小的倒正三角形。
運用類比,把正三角形變成正四面體:一個正四面體和一個倒正四面體,再各自連上線,如右下圖,這就得到了一個正十六胞體的施萊格爾投影圖。細心點數的話可以數得出,該圖中有16個四面體(包括最外部的那個),同時我們得到了正十六胞體的一些數據:
胞(正四面體)數:16,面(正三角形)數:32,棱數:24,頂點數:8 正十六胞體三維投影
正十六胞體三維投影
 正十六胞體三維投影
正十六胞體三維投影球極投影
將正十六胞體的表面膨脹使之成為一個超球,然後投影到三維上,如圖。 球極投影
球極投影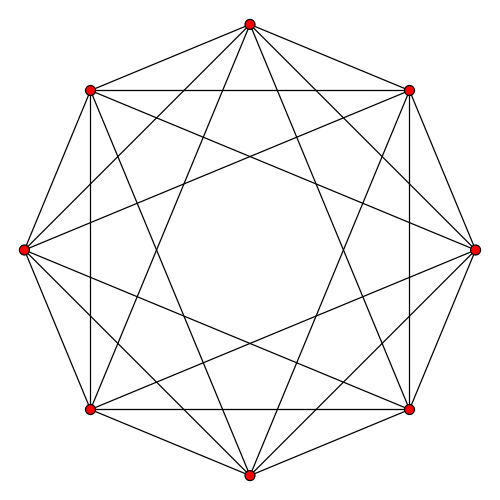 二維線架正投影
二維線架正投影
 球極投影
球極投影 二維線架正投影
二維線架正投影二維線架正投影
和超正方體的差不多,不過要簡單得多,建立一個平面上的四維投影坐標軸,寫入八個點:(±1,0,0,0)(0,±1,0,0)(0,0,±1,0)(0,0,0,±1)即可,如右圖
施萊夫利符號
正十六胞體16-cell的施萊夫利符號也有好幾個
{3,3,4}:特指它是正多胞體Hexadecachoron,以及它是Trteacross
{3^(1,1,1)}(“1,1,1”上標):特指它是n-orthoplex或n-demicube,即代指4-orthoplex和Demitesseract
h{4,3,3}:特指它是半截超立方體(alternated tesseract)
等等
類比
雖然說上去正十六胞體是正八面體的四維類比,但實際上正十六胞體可通過兩種類比方式得到
一、正八面體的類比
利用坐標,(±1,0)(0,±1)四個點連線可以得到一個正方形,即二維的正軸體
利用坐標(±1,0,0)(0,±1,0)(0,0,±1)六個點連線可以得到一個正八面體,即三維的正軸體
那么用(±1,0,0,0)(0,±1,0,0)(0,0,±1,0)(0,0,0,±1)八個點連線,就能得到這個正十六胞體,即四維的正軸體
這是一種正多胞形的類比
二、正四面體的類比
將一個正方形不相鄰的兩點連線,得到一個正二邊形(半截正方形Demisquare)
將一個立方體兩兩不相鄰的四個點沿各自的面連線,得到一個正四面體(半截立方體Demicube)線架圖
同樣地,將一個超立方體兩兩不相鄰的八個點沿各自的面連線後,則會得到正十六胞體(半截超立方體Demitesseract)的線架圖
儘管正四面體、正十六胞體,但這不是一種正多胞形的類比,在五維以及更高得到的就不是正多胞形
二胞角
對於的二胞角的求導是要用到四維解析幾何慢慢求的,太麻煩,不妨就用第一種類比法去求 二維正軸形是正方形,它的“二邊角”(也就是夾角)是90°,用反三角函式表示就是2arctan1
三維正軸形是正八面體,它的二面角約是109.47°,用反三角函式表示就是2arctan√2
那么作為四維正軸形的正十六胞體,它的二胞角用反三角函式表示就應該是2arctan√3,即120°
整數度?很神奇吧,這就是四維空間的一大魅力所在
與正八胞體聯繫
將正十六胞體中每個正四面體中心作中心所在正四面體的正三角形面垂線得正八胞體,正八胞體作類似處理也可以得正十六胞體,這種性質稱為對偶。

