基本介紹
- 中文名:正八面體
- 外文名:regular octahedron
- 頂點數:6
- 邊數:12
- 面數:8
- 套用學科:幾何學
性質


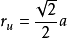


基本信息
 正八面體
正八面體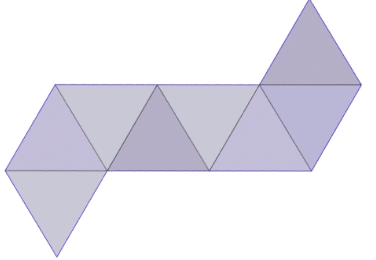 正八面體的一種展開圖
正八面體的一種展開圖坐標系
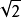
( ±1, 0, 0 )
( 0, ±1, 0 )
( 0, 0, ±1 )
正八面體表面方程為: |x|+|y|+|z|=1
更一般的,如果正八面體的對角線平行於坐標軸,中心為(x0,y0,z0),外接圓半徑為r(棱長為
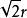
如果中心在原點的正八面體被拉長,成為菱形體,則更一般的八面體方程為





正交投影




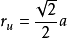


 正八面體
正八面體 正八面體的一種展開圖
正八面體的一種展開圖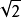
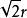






正八面體,一種正多面體,也是一種正軸體,面為8個正三角形,八面體的對角面為正方形,共三個,並且兩兩垂直。交線同樣兩兩垂直。二面角為109°28′16.3″。正...
八面體即由6個頂點與8個正三角形構成的稜錐體,有八個面,每個面都是一個等邊三角形。正如立方體一樣,八面體的這八個面均為全等的正多邊形。...
正多面體,是指多面體的各個面都是全等的正多邊形,並且各個多面角都是全等的多面角。其中面數最少的是正四面體,面數最多的是正二十面體。有些化學物質的結晶體...
八面體形分子構型指的是一個分子中,中心原子上連有六個基團或配體而形成八面體的分子構型。...
八面體構型配合物是配位數為6的配離子構型為正八面體的配合物。配體通過配位鍵與中心離子連線,分別位於中心離子的上下、前後、左右,最終的配體結構為正八面體。...
在八面體型間隙相中,6個金屬原子構成八面體,間隙原子位於八面體中心的間隙位置,具有這種間隙類型的間隙相可以是面心立方、密排六方、正交和體心立方等點陣的...
八面體應力是作用在和三個主應力軸成等傾斜面上的應力。...... 八面體應力可分為八面體正應力和八面體切應力。八面體正應力:σ0=1/3(σx+σy+σz)。...
sp3d2雜化等性雜化為正八面體結構,如SF6。在成鍵過程中,由於原子間的相互影響,同一原子中幾個能量相近的不同類型的原子軌道(即波函式),可以進行線性組合,重新...
五複合正八面體(英語:Compoundoffiveoctahedra,又稱為Octahedron5-Compound),是一種凹多面體,屬於星形多面體。這可以被看作是多面體和星形多面體的複合體。埃德蒙·...
三八面體(trioctahedron)一種特殊的正多面體.以八面體的各面為底面,向體外各作一個三側棱相等的三稜錐而得的幾何體,它是一種特殊的二十四面體.三八面體的二...
六角化八面體是卡塔蘭立體的一種,它的對偶多面體是一個阿基米德立體:大斜方截半立方體。...
釋文:八面體應力理論認為,岩土的破壞是由於八面體面上的應力達到極限值而引起的屈服破壞強度準則。1 ...
在八面體型格隙相中,6個金屬原子構成八面體,格隙原子位於八面體中心的間隙位置,具有這種格隙類型的間隙相可以是面心立方、密排六方、正交和體心立方等點陣的...
八面體空隙(octahedral void) 在等大球體的最緊密堆積中,把組成層間空隙的球心連起來,由6個球體所圍成的空隙。因其周圍6個球體中心的連線連線成八面體形狀,故...
截角八面體堆砌是三維空間內28個半正密鋪之一,由截角八面體獨立堆積而成,雖然他每個胞都全等、每邊皆等長,但其不能稱為正密鋪,因為雖然她只由一種胞,截角...
3、正方形場中d軌道能級分裂4、晶體場穩定化能(CFSE)5、姜—泰勒效應對八面體場的影響 [3] 晶體場理論分裂能 編輯 晶體場理論概念 分裂後最高能量d軌道的...
