在空間直角坐標系中,任給一點P,設r,θ是點P在xOy面上投影點的極坐標,z是點P的豎坐標,則稱(r,θ,z)是點P的柱面坐標,記為P(r,θ,z),其中r≥0,0≤θ≤2π,-∞<z<+∞ 。
基本介紹
- 中文名:柱面坐標
- 外文名:Cylindrical coordinate
- 類型:數學
- 定義:(ρ,θ,z)為M柱面坐標系
求曲面的柱面坐標方程的方法
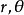

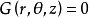
柱坐標的坐標面



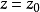

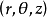
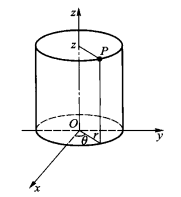 圖2
圖2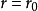
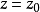
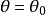
 圖3
圖3柱面坐標變換
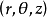
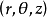

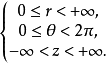
柱坐標的體積微元
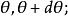
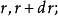



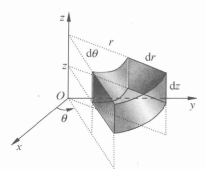 圖4
圖4柱坐標的換元公式

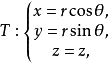
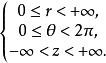
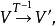
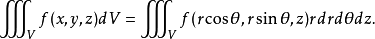
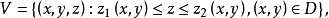
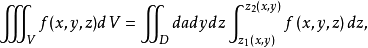
化曲面的普通方程化為柱面坐標方程
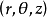

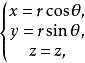

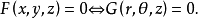


在空間直角坐標系中,任給一點P,設r,θ是點P在xOy面上投影點的極坐標,z是點P的豎坐標,則稱(r,θ,z)是點P的柱面坐標,記為P(r,θ,z),其中r≥0,0≤θ≤2π,-∞<z<+∞ 。




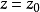

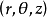
 圖2
圖2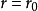
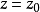
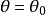
 圖3
圖3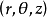
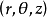

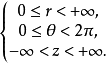
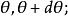
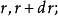



 圖4
圖4
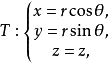
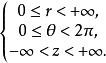
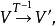
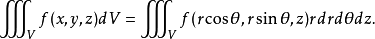
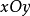
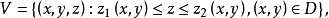
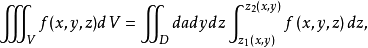
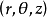

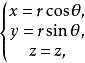

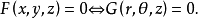

在空間直角坐標系中,任給一點P,設r,θ是點P在xOy面上投影點的極坐標,z是點P的豎坐標,則稱(r,θ,z)是點P的柱面坐標,記為P(r,θ,z),其中r≥0,0≤...
柱面坐標系是一種數據,設M(x,y,z)為空間內一點,並設點M在xoy面上的投影P的極坐標為r,θ,則這樣的三個數r, θ,z就叫點M的柱面坐標。...
圓柱坐標系是一種三維坐標系統。它是二維極坐標系往 z-軸的延伸。添加的第三個坐標 專門用來表示 P 點離 xy-平面的高低。按照國際標準化組織建立的約定 (ISO ...
柱面坐標變換是指歐氏空間中一點在柱面坐標系與標準歐氏坐標系之間的變換關係。...... 柱面坐標變換是指歐氏空間中一點在柱面坐標系與標準歐氏坐標系之間的變換關係...
柱面(cylinder)是直線沿著一條定曲線平行移動所形成的曲面,即動直線沿著一條定曲線平行移動所形成的曲面,動直線稱為柱面的直母線,定曲線稱為柱面的準線。當準線是...
圓柱坐標(cylindrical coordinates)一種空間坐標.它是.z}y平面上的極坐標與豎坐標z聯合而成的. ...
坐標系,是理科常用輔助方法。常見有直線坐標系,平面直角坐標系。為了說明質點的位置、運動的快慢、方向等,必須選取其坐標系。在參照系中,為確定空間一點的位置,按...
坐標數據是指確定平面上或空間中地麵點位置的有次序的一組數據。分為平面直角坐標數據、空間直角坐標數據、極坐標數據、球面坐標數據、柱面坐標數據和地理坐標數據等...
曲面上使兩族參數曲線彼此正交的參數系稱為曲面的正交坐標系。正交坐標系的特徵是其第一基本型的係數F≡0,因此它的第一基型成為I=Edu²+Gdv²。在曲面上...
在空間中,由平行於定方向且與一條定曲線相交的一族平行直線所生成的曲面叫做柱面。二次柱面是一種特殊的柱面,它的方程是二次的。常見的二次柱面主要包括:橢圓...
雙極圓柱坐標系(英語:Bipolar cylindrical coordinates)是一種三維正交坐標系。...... 雙極圓柱坐標系(英語:Bipolar cylindrical coordinates)是一種三維正交坐標系。...
三維笛卡兒坐標系是在二維笛卡兒坐標系的基礎上根據右手定則增加第三維坐標(即Z軸)而形成的。同二維坐標系一樣,AutoCAD中的三維坐標系有世界坐標系WCS(World ...
柱面投影變換的核心是投影變換公式,如圖(a)所示K為柱面投影空間,J表示原始圖像,J’是柱面投影圖像,坐標原點O選為圓柱中心(投影中心)。...
投射柱面(projecting cylinder)是柱面的一種,已知一條空間曲線及一個平面,以此平面的法線方向為母線方向,空間曲線為準線,所產生的柱面,叫做這條曲線關於這個平面的...
球面坐標變換是指歐氏空間中一點在球面坐標系與標準歐氏坐標系之間的變換關係。...... 系是三大常用的坐標系之一,其它二個常用的坐標系是標準的歐氏坐標系、柱面...
黃道坐標系是天球坐標系之一。黃道坐標系是以黃道為基圈〔相當於平面直角坐標系的橫軸),以經過春分點的黃經圈(半圓)為始圈(相當於平面直角坐標系的縱軸),以...
彩色坐標變換又稱彩色變換或彩色空間變換,指不同彩色系統之間的轉換。...... 坐標系統表示RGB和HSl,可導出不同的轉換模型,有柱面坐標模型、三角形模型、三角錐坐標...
