球面坐標變換是指歐氏空間中一點在球面坐標系與標準歐氏坐標系之間的變換關係。
球面坐標系




- 徑向距離是從原點到點P的歐幾里得距離。
- 傾角(或極角) θ是天頂方向和線段OP之間的夾角。
- 方位(或方位角) φ是從方位參考方向到參照平面上線段OP的正交投影的有符號角度。
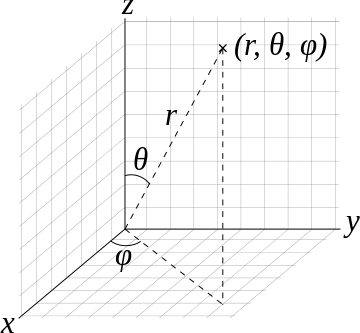 圖1
圖1


球面坐標變換




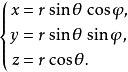

體積元




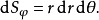


球面坐標變換是指歐氏空間中一點在球面坐標系與標準歐氏坐標系之間的變換關係。




 圖1
圖1






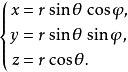





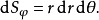


球面坐標變換是指歐氏空間中一點在球面坐標系與標準歐氏坐標系之間的變換關係。...... 球面坐標變換是指歐氏空間中一點在球面坐標系與標準歐氏坐標系之間的變換關係...
這樣的三個數r,θ,φ叫做點P的球面坐標,顯然,這裡r,θ,φ的變化範圍為r∈[0,+∞),θ∈[0, π], φ∈[0,2π] ,如圖1所示。...
球面坐標系是表示三維空間中某一點的另一種方式。它也要求三個數值,其中兩個是角度,第三個是距離。想像一條來自原點的射線(線段),它的兩個角度可以決定該射線...
坐標轉換是空間實體的位置描述,是從一種坐標系統變換到另一種坐標系統的過程。通過建立兩個坐標系統之間一一對應關係來實現。是各種比例尺地圖測量和編繪中建立地圖...
扁球面坐標是扁球面坐標系(英語:Oblate spheroidal coordinates)內的坐標。...... 坐標曲面是個扁球面, 坐標曲面是個旋轉雙曲面。從直角坐標變換至扁球面坐標:其中...
三維空間裡,有各種各樣的坐標系。球坐標系只是其中一種。球坐標系與其他坐標系的變換需要用到特別的方程式。使用以下等式,可從直角坐標變換為球坐標:...
這樣的三個數r,θ,φ叫做點P的球面坐標,顯然,這裡r,θ,φ的變化範圍為r∈[0,+∞),θ∈[0, 2π],φ∈[0, π] ,如圖1所示。...
在數學裡,球坐標系(Spherical coordinate system)是一種利用球坐標表示一個點p在三維空間的位置的三維正交坐標系。中文名 球坐標 外文名 Spherical coordinate ...
月面坐標系的一種。月球上任何一點的球面坐標以月面經度(λ)和月面緯度(β)表示。定義如下:月球自轉軸與月面交於兩點:一為月北極,北在上為正;一為月南極,...
軸正方向的夾角,因此,在空間中這些坐標的變化範圍是:在球坐標系中,坐標曲面分別是::以原點為重心, 為半徑的球面;:以 軸為邊並與坐標平面 構成角 的半平面。...
地理坐標系(Geographic Coordinate System),是使用三維球面來定義地球表面位置,以實現通過經緯度對地球表麵點位引用的坐標系。一個地理坐標系包括角度測量單位、本初...
在y2曲面和y3曲面的交線上,只有y1變化,這條交線稱為y1坐標曲線。同樣,可得y2坐標曲線和y3坐標曲線。圖1 球面坐標系(y1,y2,y3):...
一個特定的地理坐標系是由一個特定的橢球體和一種特定的地圖投影構成,其中橢球體是一種對地球形狀的數學描述,而地圖投影是將球面坐標轉換成平面坐標的數學方法。絕...
那么這種變換的從一個元素轉變到另外一個元素的對應關係,我們可以用前面的一個...(XOYZ和 X’OY’Z’的坐標系具有不為零的三個歐拉角)的球面,球面上的每一...
-坐標曲面都是不相交的圓球面。每一個圓球面都包圍著一個焦點;圓球心都包含於 z-軸。圓球半徑為它們的圓球心都包含於 z-軸。正值 的圓球面在z>0半空間;而...
坐標系、平面極坐標系、柱面坐標系(或稱柱坐標系)和球面坐標系(或稱球坐標系...如果物體沿直線運動,為了定量描述物體的位置變化,可以以這條直線為x軸,在直線上...
坐標是點 P 離兩個焦點的距離 的比例的自然對數:圓環坐標的值域為 。圓環坐標系坐標曲面 每一個 -坐標曲面都是包含了焦圓,而不同心的圓球面。圓球半徑為正...
球坐標三元數是三元數的一種,由中國超複數領域的學者白爍星首先發現和研究,...p為實數時表示兩個點±1,在p為複數時表示單位圓,在p為三元數時表示單位球面...
這樣的三個數r,φ,θ叫做點P的球面坐標,這裡r,φ,θ的變化範圍為 r∈[0,+∞), φ∈[0, 2π], θ∈[0, π] . r = 常數,即以原點為心的球面; ...
