基本介紹
- 中文名:投射柱面
- 外文名:projecting cylinder
- 所屬學科:數學
- 所屬問題:空間解析幾何
- 簡介:柱面的一種
基本介紹


相關定理

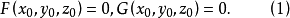



例題解析


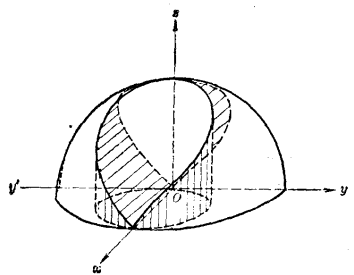 圖1
圖1
 圖4
圖4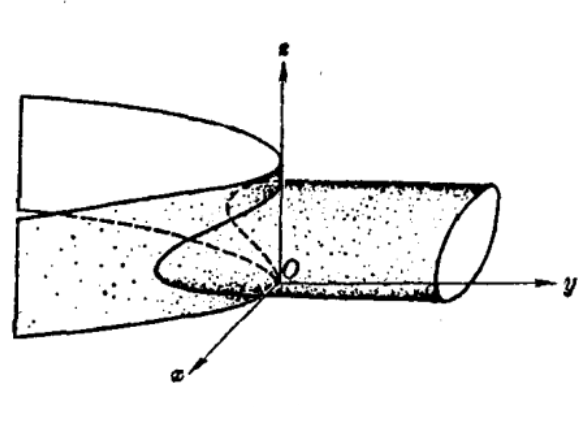



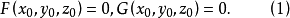





 圖1
圖1
 圖4
圖4投影柱面(projecting cylinder)是指其母線通過一條給定的曲線並且都垂直於某一坐標平面的柱面。對於給定的曲線,只要它不位於垂直於某一坐標平面的平面上,就有三個...
投射柱面(projecting cylinder)是柱面的一種,已知一條空間曲線及一個平面,以此平面的法線方向為母線方向,空間曲線為準線,所產生的柱面,叫做這條曲線關於這個平面的...
柱面投影法,是指平面圖像與柱面表面相互映射的過程,包括柱面正投影和柱面反投影。柱面正投影是指將平面圖像投影到柱面表面的過程,柱面反投影是將柱面表面的某個特定...
柱面投影變換的核心是投影變換公式,如圖(a)所示K為柱面投影空間,J表示原始圖像,J’是柱面投影圖像,坐標原點O選為圓柱中心(投影中心)。...
數虎圖像環幕影院採用內柱面投影螢幕,超寬畫面充滿觀賞者的視野,全方位立體聲與影片情節相輔相成、演繹精彩絕倫的沉浸式,融入式視聽享受。[1] ...
所以對於多通道柱面投影系統而言,解決圖像非線性失真是個關鍵問題。一般情況下,有兩種方法可以實現非線性失真校正,一種方法是通過光學校正,即通過具有獨特變形矯正功能...
UTM投影(Universal Transverse Mercator Projection--通用橫軸墨卡托投影)是橫軸等角割橢圓柱面投影。 此投影系統是美國編制世界各地軍用地圖和地球資源衛星像片所採用的...
如圖所示,假想有一個橢圓柱面橫套在地球橢球體外面,並與某一條子午線(此子午線稱為中央子午線或軸子午線)相切,橢圓柱的中心軸通過橢球體中心,然後用一定投影方法,...
地圖投影:假設用一空心橢圓柱橫套在地球橢球體上,使橢圓柱軸通過地心,橢圓柱面與橢 球體面某一經線相切;然後,用解析法使地球橢球體面上經緯網保持角度相等的關係...
高斯- 克呂格投影是一種橫軸等角切橢圓柱投影。這種投影是將一橢圓柱面套在地球橢球的外面,並與某一子午線相切(此子午線叫中央子午線或中央經線),橢圓中心軸通過...
構想用一個橢圓柱橫切於橢球面上投影帶的中央子午線,按上述投影條件,將中央子午線兩側一定經差範圍內的橢球面正形投影於橢圓柱面。將橢圓柱面沿過南北極的母線剪開...
將橢圓柱面沿過南北極的母線剪開展平,即為高斯投影平面。取中央子午線與赤道交點的投影為原點,中央子午線的投影為縱坐標x軸,赤道的投影為橫坐標y軸,構成高斯克呂...
