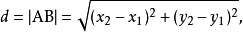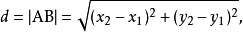定義
坐標幾何包括
平面解析幾何和立體解析幾何兩部分。平面
解析幾何通過平面
直角坐標系,建立點與
實數對之間的一一對應關係,以及
曲線與方程之間的一一對應關係,運用
代數方法研究幾何問題,或用幾何方法研究代數問題。
解析幾何(英語:
Analytic geometry),又稱為
坐標幾何(英語:
Coordinate geometry)或
卡氏幾何(英語:
Cartesian geometry),早先被叫作
笛卡兒幾何,是一種藉助於解析式進行圖形研究的幾何學分支。解析幾何通常使用二維的平面直角坐標系研究直線、圓、圓錐曲線、擺線、星形線等各種一般平面曲線,使用三維的
空間直角坐標系來研究
平面、
球等各種一般空間曲面,同時研究它們的
方程,並定義一些圖形的概念和參數。
歷史
古希臘數學家梅內克繆斯(Menaechmus)的解題、證明方式與現在使用坐標系十分相似,以至於有時會認為他是解析幾何的鼻祖。阿波羅尼奧斯在《論切觸》中解題方式在現在被稱之為單維解析幾何;他使用直線來求得一點與其它點之間的比例。阿波羅尼奧斯在《圓錐曲線論》中進一步發展了這種方式,這種方式與解析幾何十分相似,比起笛卡兒早了1800多年。他使用了參照線、直徑、切線與現進所使用坐標系沒有本質區別,即從切點沿直徑所量的距離為橫坐標,而與切線平行、並與數軸和曲線向交的線段為縱坐標。他進一步發展了橫坐標與縱坐標之間的關係,即兩者等同於誇張的曲線。然而,阿波羅尼奧斯的工作接近於解析幾何,但它沒能完成它,因為他沒有將負數納入系統當中。在此,方程是由曲線來確定的,而曲線不是由方程得出的。坐標、變數、方程不過是一些給定幾何題的腳註罷了。
十一世紀波斯帝國數學家歐瑪爾·海亞姆發現了幾何與代數之間的密切聯繫,在求三次方程使用了代數和幾何,取得了巨大進步。但最關鍵的一步由笛卡兒完成。
從傳統意義上講,解析幾何是由勒內·笛卡兒創立的。笛卡兒的創舉被記錄在《幾何學》(
La Geometrie)當中,在1637年與他的《方法論》一道發表。這些努力是以法語寫成的,其中的哲學思想為創立
無窮小提供了基礎。最初,這些著作並沒有得到認可,部分原因是由於其中論述的間斷,方程的複雜所致。直到1649年,著作被翻譯為拉丁語,並被馮·斯霍滕(van Schooten)恭維後,才被大眾所認可接受。
費馬也為解析幾何的發展做出了貢獻。他的《平面與立體軌跡引論》(
Ad locos planos et solidos isagoge)雖然沒有在生前發表,但手稿於1637年在巴黎出現,正好早於笛卡兒《方法論》一點。《引論》文字清晰,獲得好評,為解析幾何提供了鋪墊。費馬與笛卡兒方法的不同在於出發點。費馬從代數公式開始,然後描述它的幾何曲線,而笛卡兒從幾何曲線開始,以方程的完結告終。結果,笛卡兒的方法可以處理更複雜的方程,並發展到使用高次多項式來解決問題。
發展
17世紀以來,由於
航海、
天文、
力學、
經濟、
軍事、
生產的發展,以及初等幾何和
初等代數的迅速發展,促進了坐標幾何的建立,並被廣泛套用於
數學的各個分支。在坐標幾何創立以前,幾何與代數是彼此獨立的兩個分支。坐標幾何的建立第一次真正實現了幾何方法與代數方法的結合,使形與數統一起來,這是
數學發展史上的一次重大突破。作為變數數學發展的第一個決定性步驟,坐標幾何的建立對於
微積分的誕生有著不可估量的作用。
基本理論
坐標
在解析幾何當中,平面給出了坐標系,即每個點都有對應的一對實數坐標。最常見的是
笛卡兒坐標系,其中,每個點都有
x-坐標對應水平位置,和
y-坐標對應垂直位置。這些常寫為
有序對(
x,
y)。這種系統也可以被用在三維幾何當中,空間中的每個點都以
多元組呈現(
x,
y,
z)。
坐標系也以其它形式出現。在平面中最常見的另類坐標系是
極坐標系,其中每個點都以從原點出發的
半徑r和角度
θ表示。在三維空間中,最常見的另類坐標系統是
圓柱坐標系和
球坐標系。
曲線方程
在解析幾何當中,任何方程都包含確定面的
子集,即方程的解集。例如,方程
y=
x在平面上對應的是所有
x-坐標等於
y-坐標的解集。這些點匯集成為一條直線,
y=
x被稱為這道方程的直線。總而言之,線性方程中
x和
y定義線,一元二次方程定義圓錐曲線,更複雜的方程則闡述更複雜的形象。
通常,一個簡單的方程對應平面上的一條曲線。但這不一定如此:方程x=x對應整個平面,方程x2+y2=0 只對應(0,0)一點。在三維空間中,一個方程通常對應一個曲面,而曲線常常代表兩個曲面的交集,或一條參數方程。方程x2+y2=r2代表了是半徑為r且圓心在(0, 0)上的所有圓。
距離和角度
在解析幾何當中,距離、角度等幾何概念是用
公式來表達的。這些定義與背後的
歐幾里得幾何所蘊含的主旨相符。例如,使用平面
笛卡兒坐標系時,兩點A(
x1,
y1),B(
x2,
y2)之間的距離
d(又寫作
|AB
|被定義為
上述可被認為是一種
勾股定理的形式。類似地,直線與水平線所成的角可以定義為
變化
變化可以使母方程變為新方程,但保持原有的特性。例如,母方程
有水平和垂直的漸近線,處在第一和第三象限當中能夠,它所有的變形都有水平和垂直的漸近線,出現在第一或第三、第二或第四象限當中。總的來說,如果y=f(x),那么它可以變為y=af[b(x-k)]+h。新的變形方程,a因素如果大於1,就垂直拉伸方程;如果小於1,就壓縮方程。如果a 值為負,那么方程就反映在 x-軸上。 b值如果大於1就水平壓縮方程,小於1就拉伸方程。與a一樣,如果為負就反映在y-軸上。k和 h 值為平移,h值是垂直,k 為水平。h 和 k 的正值意味著方程往數軸的正方向移動,負值意味這往數軸的負方向移動。
變化可以套用到任意幾何等式中,不論等式是否代表某一方程。 變化可以被認為是個體處理、或是組合處理。
交集
雖然本討論僅限於xy-平面上,但它可以很容易地衍生為更高維的空間中。兩個幾何對象P 和 Q 指代P(x,y) 和Q(x,y),其交集是所有點(x,y) 的集合。
截距
被廣泛研究的一種交集是幾何對象與 x 和y 坐標軸的交集。
幾何對象與y-軸的交集被稱之為對象的 y-
截距。與 x-軸的交集被稱之為對象的 x-截距。
就線 y=mx+b而言,參數b定義線在何處與 y軸相交。據此, b 或(0,b) 點被稱之為 y-截距。
套用
解析幾何中的重要問題:
現代解析幾何
解析簇(analytic variety)定義為幾個
解析函式的共同解集。類似與實數與複數的代數簇。任何複流形都是一種解析簇。由於解析簇可能有奇點,但不是所有解析簇都是複數。.
解析幾何總體上來說等同與實數與複數代數幾何,讓-皮埃爾·塞爾在他的著作《代數幾何與解析幾何》(Géometrie Algébrique et Géométrie Analytique)闡述了這個觀點。然而,兩個領域依然有其獨特性,而證明方式也十分不同,代數幾何也包括幾何的有限特徵。