基本介紹
- 中文名:圓錐曲線系
- 概念:具有某種共同性質的圓錐曲線
- 領域:數學
- 分類:同心圓系、同焦點圓錐曲線系等
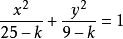
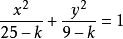
具有某種共同性質的圓錐曲線稱為“圓錐曲線系”。例如,在方程x²+y²=r²中,給任意常數r(r>0)以不同的數值時,就得到一系列的圓,則由它們組成了以原點...
圓錐曲線,是由一平面截二次錐面得到的曲線。圓錐曲線包括橢圓(圓為橢圓的特例)、拋物線、雙曲線。起源於2000多年前的古希臘數學家最先開始研究圓錐曲線。圓錐曲線(...
共焦有心圓錐曲線族(family of the confocalcentral conics)是一類圓錐曲線的集合。圓錐曲線亦稱圓錐截線。簡稱錐線。一類重要的二次曲線。它是不過圓錐頂點的平面...
《高考數學你真的掌握了嗎?圓錐曲線》是2014年清華大學出版社出版的圖書,作者是張楊文、蘭師勇。...
《圓錐曲線結構思想與解題策略》是由聞傑編寫,浙江大學出版社出版的一本書籍。...... 《圓錐曲線結構思想與解題策略》是由聞傑編寫,浙江大學出版社出版的一本書籍。...
通徑:2P ;定義:圓錐曲線(除圓外)中,過焦點並垂直於軸的弦定義域:對於拋物線y2=2px,p>0時,定義域為x≥0,p<0時,定義域為x≤0;對於拋物線x2=2py,定義...
Apollonius 所著的八冊《圓錐曲線》(Conics)集其大成,可以說是古希臘解析幾何學一個登峰造極的精擘之作。今日大家熟知的 ellipse(橢圓)、parabola(拋物線)、hyperbo...
弦長公式,在這裡指直線與圓錐曲線相交所得弦長d的公式。PS:圓錐曲線, 是數學、幾何學中通過平切圓錐(嚴格為一個正圓錐面和一個平面完整相切)得到的一些曲線,如:...
解析幾何通常使用二維的平面直角坐標系研究直線、圓、圓錐曲線、擺線、星形線等各種一般平面曲線,使用三維的空間直角坐標系來研究平面、球等各種一般空間曲面,同時研究...
