基本介紹
- 中文名:垂足三角形
- 外文名:pedal triangle
- 所屬學科:數學
- 定義:銳角三角形三邊的垂足形成三角形
- 相關概念:垂足,內接三角形等
定義




 圖1
圖1相關結論
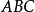















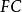

 圖2
圖2

 圖3
圖3




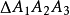


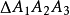
 圖4
圖4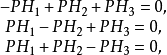





 圖5
圖5




 圖1
圖1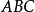















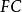

 圖2
圖2

 圖3
圖3




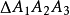


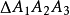
 圖4
圖4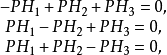





 圖5
圖5垂足三角形(pedal triangle)是一種特殊三角形,指從三角形的三個頂點向對邊作垂線段(即高),連結三個垂足所得的三角形。...
施瓦茲三角形問題(Schwarz triangle problem)是關於三角形的極值問題,在銳角三角形的內接三角形中,以垂足三角形的周長為最短,此問題最早由法尼亞諾(dei.T.G.C....
三角形五心是指三角形的重心、外心、內心、垂心、旁心。三條中線的交點是重心,三邊垂直平分線的交點是外心,三條內角平分線的交點為內心,三角形三條高線的交點為...
切線三角形(tangent triangle)是一種特殊三角形,指從三角形的各頂點作外接圓切線所成的三角形稱為切線三角形。切線三角形是外接圓的極三角形。...
給定△ABC及其平面上不在三角形邊上的一點P,聯結AP,BP,CP交對應邊於A',B',C',則△A'B'C'稱為P點關於△ABC的切瓦三角形(Cevian Triangle)。...
三角形的三條高線的交點叫做三角形的垂心。銳角三角形的垂心在三角形內;直角三角形的垂心在直角頂點上;鈍角三角形的垂心在三角形外...
三角形的四心是指三角形的重心、外心、內心、垂心。若且唯若三角形是正三角形的時候,重心、垂心、內心、外心四心合一心,稱做正三角形的中心。...
中點三角形就是把一個三角形的三邊中點順次連線起來的一個新三角形,與原三角形相似。...
《近代的三角形幾何學》是平面歐氏幾何學的經典之作。以三線坐標和重心坐標為工具,對內接外切的三角形族、西摩松線、垂足三角形、垂極點、逆垂足三角形、三角形...
給定一個三角形,按此三角形的某些關係構成的新三角形稱之為該三角形的伴隨三角形。...... 常見的伴隨三角形垂三角形、中位三角形、垂足三角形、旁心三角形V百科...
在數學中,三角形的高線(或稱高、垂線)是過它的一個頂點的垂直於對邊的直線,或這條直線上從頂點到與對邊交點之間的線段。高線與對邊的交點稱為垂足。過一個...
由一個三角形的各個頂點向任一條直線作垂線,則由其垂足向對邊所作垂線必交於一點,稱為這條直線的垂極點。當直線平行移動時,垂極點的軌跡是與它垂直的直線。...
在幾何學中,一個垂心組是由四個點組成的平面圖形。使得其中一點都是另外三點組成的三角形的垂心。由三角形的三頂點及垂心引發人們給出垂心組的概念:以三點為...
幾何學中,設點 P 是三角形 ABC 平面上一點,作直線 PA、PB 和 PC 分別關於角 A 、B 和 C 的平分線的反射,這三條反射線必然交於一點,稱此點為 P ...
格雷貝作圖法(Grebe construction method)是求作三角形的陪位重心的一種方法。自三角形△ABC各邊向外作正方形得正方形BCPP′,CAQQ′和ABRR′,設QQ′與RR′,...
旁心,三角形五心之一(其他四個為內心、外心、重心和垂心)。旁心是三角形的旁切圓(與三角形的一邊和其他兩邊的延長線相切的圓)的圓心。...
費爾巴哈定理描述了三角形的九點圓與其內切圓以及三個旁切圓的位置關係。是平面幾何學中十分優美的定理之一。...
熱爾崗點(Gergonne point)是三角形三條特殊直線的交點,若X,Y,Z分別是△ABC的三邊BC,CA,AB與其內切圓或旁切圓的切點,則三線AX,BY,CZ共點,這樣的點共有四...
九點圓(又稱歐拉圓、費爾巴哈圓),在平面幾何中,對任何三角形,九點圓通過三角形三邊的中點、三高的垂足和頂點到垂心的三條線段的中點。九點圓定理指出對任何三角...
《近代歐氏幾何學》是1998年由上海教育出版社出版的圖書,該書作者是(美)詹森。本書探討了三角形和圓形的幾何結構,主要專注於歐氏理論的延伸並詳細地研究了許多...
