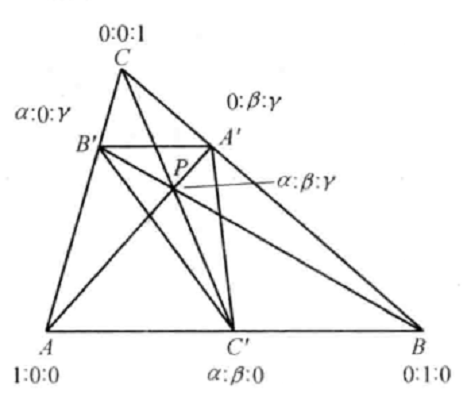
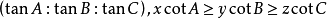給定△ABC及其平面上不在三角形邊上的一點P，聯結AP，BP，CP交對應邊於A'，B'，C'，則△A'B'C'稱為P點關於△ABC的切瓦三角形(Cevian Triangle)。
基本介紹
- 中文名：切瓦三角形
- 外文名：Cevian Triangle
- 所屬學科：數學
- 相關概念：切瓦圓，外接切瓦三角形等
- 舉例：內心三角形，垂足三角形等
基本介紹,定義,切瓦三角形的三條邊長,切瓦三角形的面積,切瓦三角形的周長,切瓦圓,外接三角形與半切瓦三角形,外接切瓦三角形,半切瓦三角形,
基本介紹
定義
給定
及其平面上但不在三角形邊上的一點P，聯結AP，BP，CP交對應邊於A'，B'，C'，則
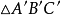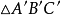
稱為P點關於 的切瓦三角形(Cevian Triangle)，如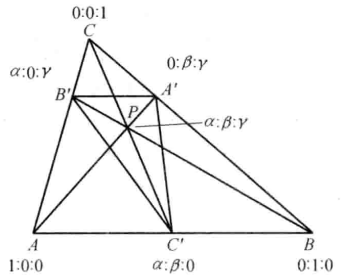圖1。
圖1切瓦三角形的三條邊長
設P點的三線坐標是
則切瓦三角形各頂點的三線坐標矩陣是
切瓦三角形的面積
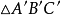
切瓦三角形的周長
下面來討論一下切瓦三角形的周長。
定理1 考慮一個三角形ABC，其邊長
，定義
是BC，CA，AB邊上的中點，設D，E，F是BC，CA，AB邊上的點，且滿足下列條件：
(1.1) D在X和C之間，E在Y和C之間，F在Z和B之間。
(1.2) ∠CDE≤∠BDF，∠CED≤∠AEF，∠BFD≤∠AFE，那么∠DEF的周長不大於△ABC的半周長如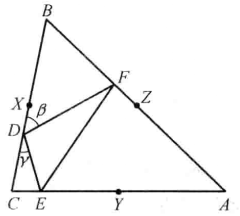圖2。
圖2定理2 假定三角形ABC邊長滿足 ，設P在三角形內，P有正號的齊次重心坐標
，且滿足：
(2.1)
；
(2.2)
，
那么P點的切瓦三角形的周長不大於△ABC的中點三角形的周長。
作為例子，內心有重心坐標
，條件(2.1) 實際變為
對於形心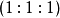
，也有
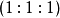
可見這些點都滿足條件(2.1)。
至於奈格爾點，
能滿足條件(2.2)，但不滿足條件(2.1)，外心也同樣如此。
切瓦圓
切瓦三角形的外接圓稱為切瓦圓。表1是一些常見的幾何特徵點所對應的切瓦三角形及切瓦圓。
外接三角形與半切瓦三角形
由切瓦三角形又衍生出兩個概念：一是外接切瓦三角形；二是半切瓦三角形。
外接切瓦三角形
給出△ABC及其平面上但不在三角形邊上的一點P，聯結AP，BP，CP，交△ABC的外接圓於A'，B'，C'，則△A'B'C'稱為P點關於△ABC的外接切瓦三角形，如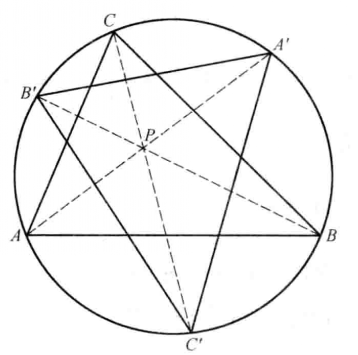圖3。
圖3當P的三線坐標是時，外接切瓦三角形的各頂點的三線坐標矩陣是
當P點分別是△ABC的內心、形心和垂心時，其外接切瓦三角形分別是：外接中點弧三角形，外接中點三角形，外接垂足三角形。
P的外接切瓦三角形與P點的垂足三角形相似。
半切瓦三角形
衍生出的第二個概念是半切瓦三角形(Half-cevian Triangle)。
若
是P點關於△ABC的切瓦三角形，取
的中點
，則
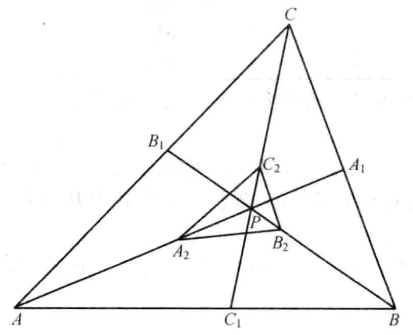，則稱為是P點關於△ABC的半切瓦三角形，如圖4。
圖4