切線三角形

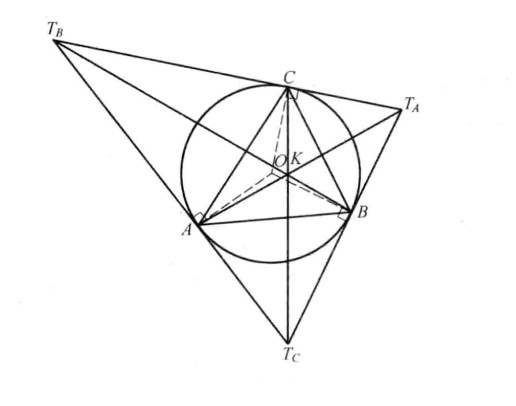
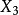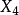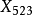切線三角形(tangent triangle)是一種特殊三角形，指從三角形的各頂點作外接圓切線所成的三角形稱為切線三角形。切線三角形是外接圓的極三角形。

基本介紹

• 中文名：切線三角形
• 外文名：tangent triangle
• 所屬學科：數學（平面幾何）
• 相關概念：外接圓，切線
• 性質：切線三角形是外接圓的極三角形

基本概念

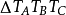
過△ABC的各個頂點作其外接圓的切線，三切線兩兩相交於 ， 是△ABC的切線三角形(Tangential Triangle)。它是△ABC外心O的反垂足三角形，也是△ABC的共軛重心的反切瓦三角形，如圖1。

圖1

相關性質及定理

① △ABC中的共軛重心就是 的熱爾崗點。

② 切線三角形是外接圓的極三角形。

③ 切線三角形的三線坐標矩陣是

其各邊的邊長是

其面積是

④ 表1中列出了切線三角形內的特徵點與原三角形內特徵點的對應關係。

表1

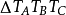
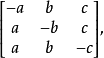
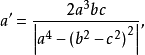
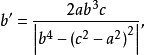
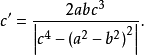
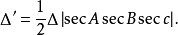
切線三角形中的特徵點	原△ABC內的特徵點
重心	對 的切瓦共軛點
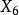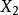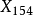外心	切線三角形的外心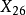
垂心	垂足三角形的本徵中心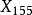
九點圓圓心	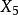切線三角形中的 ( )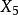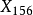
共軛重心	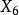切線三角形中的 ( )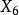
歐拉無窮遠點	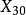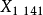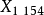的等角共軛點
的等角共軛點	拿破崙交叉差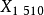

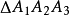
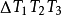
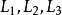
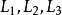
⑤ 給定 和它的切線三角形 ，兩三角形的三條邊兩兩相交於 ，則 共線，如圖2。

圖2（a）

圖2（b） (a)的放大圖

⑥ 切線三角形的外接圓稱為切線圓，它的圓心是

其半徑是

⑦ 下面介紹一個有關切線三角形的定理：

設△ABC的切線三角形是△A'B'C'，設A"，B"，C"是在△ABC外接圓上的任意三點，則有

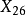
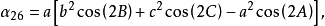
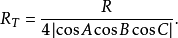
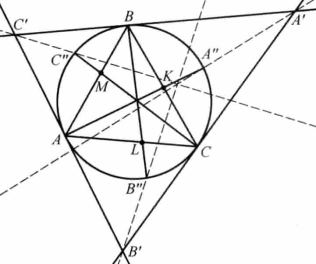定理1(斯坦巴特(Stein bart)) 若且唯若直線AA”，BB"和CC"共點，或AA”∩BC，BB"∩CA，CC"∩AB共線時，A'A"，B'B"和C'C"共點，如圖3。

圖3