內接三角形(inscribed triangle)是一種幾何圖形。如果圓O上有三個互不重合的點A、B、C,則這三點構成的△ABC叫做"圓O的內接三角形" 。
基本介紹
- 中文名:內接三角形
- 外文名:inscribed triangle
- 所屬學科:數學
- 定義:三頂點都在一個圓周上的三角形
- 相關概念:外接圓、中垂線等
- 相似概念:外切三角形、內接圓等
定義
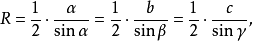
相關證明題舉例
 圖1
圖1

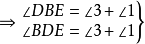
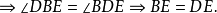
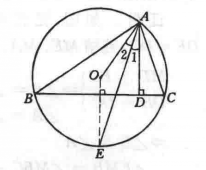 圖2
圖2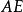
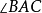
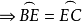
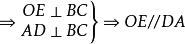
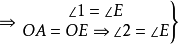

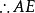
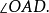
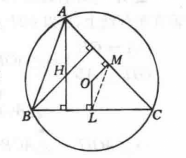 圖3
圖3
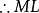
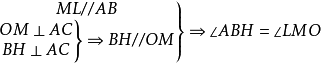
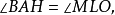
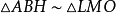
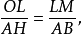

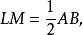
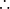
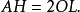

內接三角形(inscribed triangle)是一種幾何圖形。如果圓O上有三個互不重合的點A、B、C,則這三點構成的△ABC叫做"圓O的內接三角形" 。
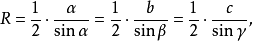
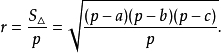
 圖1
圖1

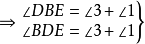
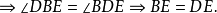
 圖2
圖2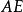
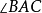
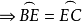
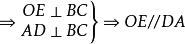
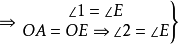

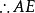
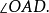
 圖3
圖3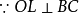
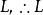
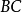
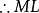
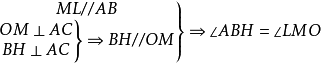
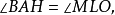
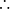

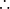
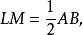
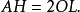
內接三角形(inscribed triangle)是一種幾何圖形。如果圓O上有三個互不重合的點A、B、C,則這三點構成的△ABC叫做"圓O的內接三角形" 。...
三角形的一個角等於它所對的邊與圓心相連所形成的夾角的一半...... 在同圓或等圓內,三角形的三個頂點均在同一個圓上的三角形叫做圓內接三角形。...
與三角形三邊都相切的圓叫做三角形的內切圓,圓心叫做三角形的內心,三角形叫做圓的外切三角形,三角形的內心是三角形三條角平分線的交點。...
若四邊形的四個頂點都在三角形的邊上,則稱該四邊形為此三角形的內接四邊形.特別地,當該四邊形為矩形時,稱此四邊形為此三角形的內接矩形...
施瓦茲三角形問題(Schwarz triangle problem)是關於三角形的極值問題,在銳角三角形的內接三角形中,以垂足三角形的周長為最短,此問題最早由法尼亞諾(dei.T.G.C....
三角形五心是指三角形的重心、外心、內心、垂心、旁心。三條中線的交點是重心,三邊垂直平分線的交點是外心,三條內角平分線的交點為內心,三角形三條高線的交點為...
三角形的三條高線的交點叫做三角形的垂心。銳角三角形的垂心在三角形內;直角三角形的垂心在直角頂點上;鈍角三角形的垂心在三角形外...
三角形的四心是指三角形的重心、外心、內心、垂心。若且唯若三角形是正三角形的時候,重心、垂心、內心、外心四心合一心,稱做正三角形的中心。...
如圖2,AB為圓O的切線,因為BD是直徑,所以內接三角形BCD是直角三角形,其中∠DCB是直角所以∠BDC+∠1=90°又因為∠1 +∠CBA=90°所以∠CBA=∠BDC....
