費爾巴哈定理

費爾巴哈定理描述了三角形的九點圓與其內切圓以及三個旁切圓的位置關係。是平面幾何學中十分優美的定理之一。

基本介紹

• 中文名：費爾巴哈定理
• 外文名：Feuerbach’s law
• 提出者：費爾巴哈
• 套用學科：數學
• 適用領域範圍：平面幾何

定理敘述

三角形的九點圓與其內切圓以及三個旁切圓相切。

定理證明

設△ABC的內心為I，九點圓的圓心為V。三邊中點分別為L，M，N，內切圓與三邊的切點分別是P，Q，R，三邊上的垂足分別為D，E，F。

不妨設AB>AC。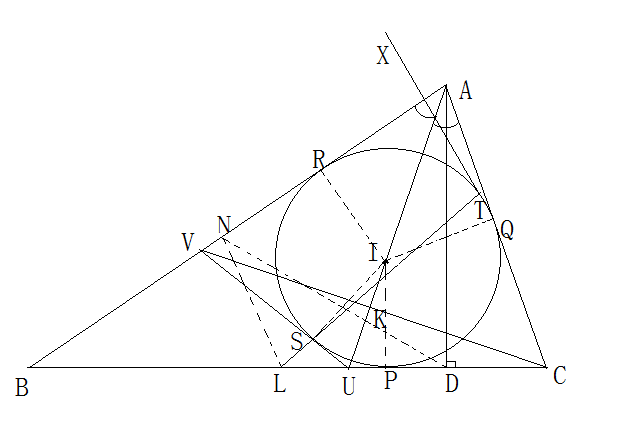

全局圖

假設⊙I與⊙V相切於點T，那么LT與⊙I相交，設另一個交點為S。

過點S作⊙I的切線，分別交AB和BC於V，U，連線AU。

又作兩圓的公切線TX，使其與邊AB位於LT的同側。

由假設知

∠XTL=∠LDT

而TX和SV都是⊙I的切線，且與弦ST所夾的圓弧相同，於是

∠XTL=∠VST

因此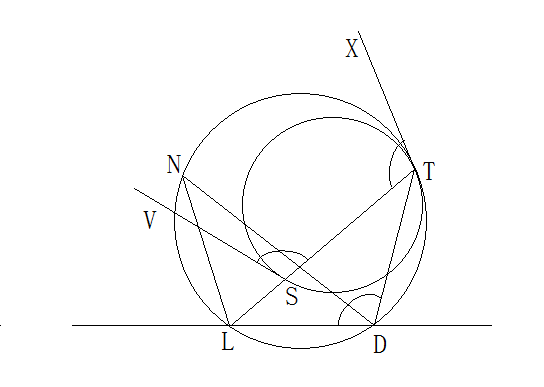

局部圖1

∠LDT=∠VST

則

∠UDT+∠UST=180°

這就是說，S，T，D，U共圓。

而這等價於：LU×LD=LS×LT

又 LP²=LS×LT

故有 LP²=LU×LD

另一方面，T是公共的切點，自然在⊙V上，

因此 L，D，T，N共圓，進而有

∠LTD=∠LND

由已導出的S，T，D，U共圓，得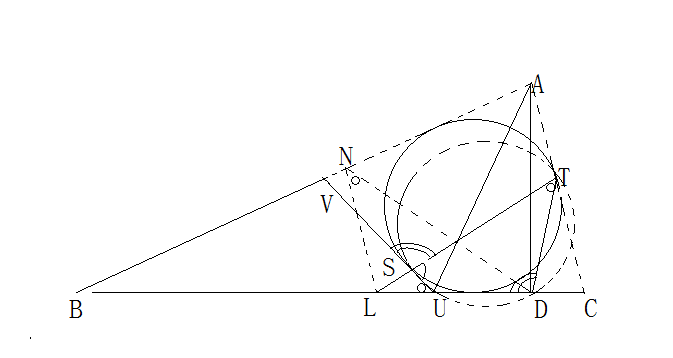

局部圖2

∠LTD=∠STD=180°-∠SUD=∠VUB

=∠AVU-∠B

而

∠LND=∠NLB-∠NDB

=∠ACB-∠NBD

=∠C-∠B

（這裡用了LN∥AC，以及直角三角形斜邊上中線等於斜邊的一半）

所以，就得到

∠AVU=∠C

注意到AV，AC，CU，UV均與⊙I相切，於是有

∠AIR=∠AIQ

∠UIS=∠UIP

∠RIS=∠QIS

三式相加，即知

∠AIU=180°

也即是說，A，I，U三點共線。

另外，AV=AC，這可由△AIV≌△AIC得到。

（這說明，公切點T可如下得到：

連線AI，並延長交BC於點U，

過點U作⊙I的切線，切點為S，交AB於V，

最後連線LS，其延長線與⊙I的交點即是所謂的公切點T。

）

連線CV，與AU交於點K，

則K是VC的中點。

前面已得到：LP²=LU×LD

而

2LP=(BL+LP)-(CL-LP)

=BP-CP

=BR-CQ

=(BR+AR)-(CQ+AQ)

=AB-AC

=AB-AV

=BV

即 LP=BV

然而

LK是△CBV的中位線

於是 LK=BV

因之 LP=LK

故 LK²=LU×LD

由於以上推導均可逆轉，因此我們只需證明： LK²=LU×LD。往證之

這等價於：LK與圓KUD相切

於是只需證：∠LKU=∠KDU

再注意到 LK∥AB（LK是△CBV的中位線），即有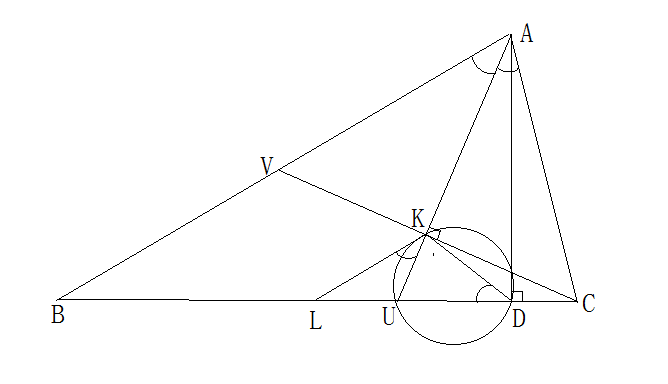

局部圖3

∠LKU=∠BAU

又AU是角平分線，於是

∠LKU=∠CAU=∠CAK

於是又只需證：∠CAK=∠KDU

即證：∠CAK+∠CDK=180°

這即是證：A，C，D，K四點共圓

由於 AK⊥KC（易得），AD⊥DC

所以 A，C，D，K確實共圓。

這就證明了⊙I與⊙V內切。

旁切圓的情形是類似的。

證畢

另略證：

OI^2=R^2-2Rr

IH^2=2r^2-2Rr'

OH^2=R^2-4Rr'(其中r‘是垂心H的垂足三角形的內切圓半徑，R、r是三角形ABC外接圓和內切圓半徑)

FI^2=1/2(OI^2+IH^2)-1/4OH^2=(1/2R-r)^2

FI=1/2R-r這就證明了九點圓與內切圓內切（九點圓半徑為外接圓半徑一半。F是九點圓圓心，I為內心）