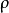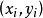定義在曲面上的函式關於該曲面的積分。第一型曲線積分物理意義來源於對給定密度函式的空間曲面,計算該曲面的質量。
基本介紹
- 中文名:第一型曲面積分
- 又稱:對面積的曲面積分
- 相關書籍:數學分析
- 物理意義:空間曲面S的“質量”
定義,計算,物理意義,性質,套用,
定義
設 為空間中的曲面,
為空間中的曲面, 為定義在
為定義在 上的函式.對曲面
上的函式.對曲面 作分割
作分割 ,它把分成
,它把分成 個可求面積的小曲面片
個可求面積的小曲面片 ,
, 的面積記為
的面積記為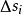 ,分割
,分割 的細度為
的細度為 ,在
,在 上任取一點
上任取一點 , 若存在極限
, 若存在極限








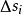





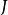
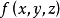


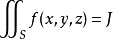
計算
設空間曲面S的方程為 ,
,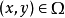 ,其中
,其中  為曲面S在
為曲面S在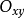 平面上的投影域,函式
平面上的投影域,函式 在曲面S上連續,如果
在曲面S上連續,如果 在
在 上有連續的一階偏導數,則有
上有連續的一階偏導數,則有

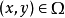

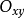






物理意義
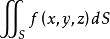



性質
第一型曲面積分具有下述一些重要性質:
1).若 存在,
存在, 為常數,則
為常數,則 也存在,且
也存在,且




2).若曲面 由互不相交的曲面塊
由互不相交的曲面塊 組成,且
組成,且 都存在,則
都存在,則 也存在,且
也存在,且





3).若 與
與 都存在,且在
都存在,且在 上
上 , 則
, 則





4).若 存在,則
存在,則 也存在,且
也存在,且



套用
下面給出二個常用的套用。
1)空間曲面S的重心坐標為

2)曲面S繞z軸(x, y軸)的轉動慣量是

其中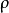 為曲面的密度函式。
為曲面的密度函式。