弗羅貝尼烏斯態射(Frobenius morphism)是特徵p的概形上特有的態射。設k是一個特徵p>0的域。對任意一個k上的概形X,可以定義一個X到自身的態射FX:X→X,它把每個點映到自身,而把每個(定義在開子集上的)函式映成自身的p次冪。FX稱為X的絕對弗羅貝尼烏斯態射。
基本介紹
- 中文名:弗羅貝尼烏斯態射
- 外文名:Frobenius morphism
- 領域:數學
- 學科:範疇論
- 概念:特徵p的概形上特有的態射
- 提出者:弗羅貝尼烏斯
弗羅貝尼烏斯,態射,概形,
概念
弗羅貝尼烏斯態射(Frobenius morphism)是特徵p的概形上特有的態射。設k是一個特徵p>0的域。對任意一個k上的概形X,可以定義一個X到自身的態射FX:X→X,它把每個點映到自身,而把每個(定義在開子集上的)函式映成自身的p次冪。FX稱為X的絕對弗羅貝尼烏斯態射。設S是K概形,而X是S概形。做纖維積,於是存在惟一的S態射FX/S:X→X,使得σ°FX/S=FX.FX/S,稱FX/S為X在S上的相對弗羅貝尼烏斯態射。絕對弗羅貝尼烏斯態射和相對弗羅貝尼烏斯態射統稱弗羅貝尼烏斯態射。弗羅貝尼烏斯態射是典範的,即對任何K概形的態射f:X→Y,有下面的圖交換。
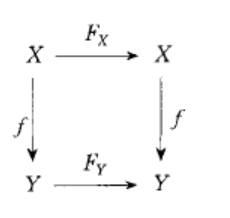 圖1 絕對態射
圖1 絕對態射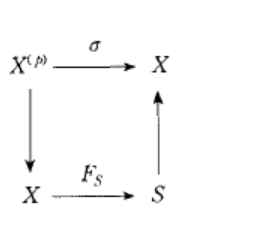 圖2 相對態射
圖2 相對態射弗羅貝尼烏斯
德國數學家。生於柏林,卒於柏林夏洛滕堡(Ch arlottenburg)。1867年在哥廷根學習數學。1870年獲博士學位,1874年任柏林大學教授。1893年當選為柏林普魯士科學院院士。他的研究涉及群論的三個方面:代數方程的解,包括伽羅瓦理論的置換群;②幾何,與有窮和無窮變換群及李群相聯繫;③數論,用到二次型的複合與加法群。代表作有《關於可換元素群》(Ueber Gru ppen von vertauschbaren Elementen,1879)、《有限群》(Uber endliche Gruppen,1895)和《群特徵標》(U-ber die Gruppencharaktere,1896)等。論述的核心是群的特徵理論,為此引入“秩”的概念。還研究了特徵多項式,不變因子和初等因子的性質。這種理論有著廣泛的適用性,解決了一大批長期以來懸而未決的問題。另外,他在超複數系,微分方程的級數解、解析函式的冪級數和發散級數等方面也有建樹。福賽思(Forsyth,Andrew Russell,1858.6.18—1942.6.2) 英國數學家。生於蘇格蘭格拉斯哥(Glasgow),卒於倫敦。1877年就學於劍橋三 一學院。是凱萊的學生。1881年畢業時以數學優異成績留校執教,次年主持利物浦大學學院數學講座。1884年回劍橋任教。兩年後當選為皇家學會會員。他的名作《函式論》(Theory of Functions,1893)被認為是自牛頓《原理》以來對英國數學影響較大的專著之一,為數學現代化起了引導作用。另外著有《變分學》(Calculusof Variations,1927)、《理想空間的內蘊幾何學》(Intrinsic Geometryof Ideal Space,1935)等書。
態射
態射是範疇論的基本概念之一。通常可看成是同態與映射的推廣。
範疇論是代數學的一個重要分支。數學的各個領域都有各自的研究對象。例如,集合論研究集合與映射;線性代數研究線性空間與線性映射;群論研究群與群同態;拓撲學研究拓撲空間與連續映射。在20世紀中期,數學家們認為有必要將各個領域中的研究對象各自合在一起成為一個整體,使之成為一種數學系統,這就是範疇思想。於是,所有的集合與映射組成集合範疇;所有的群與群同態組成群範疇。在各個範疇之間往往存在著內在聯繫與變換。例如,一個群模去其換位子群的商群(稱為交換化)得到一個交換群,從而交換化成為群範疇到交換群範疇的一個變換,且這個變換保持著群同態及其合成。事實上,這就是函子的思想.在域F上的線性空間範疇中,任一線性空間L必有惟一的對偶空間L=HomF(L,F),“*”可看成這個線性空間範疇到自身的一個變換。儘管當L為有限維時L與L是同構的(記這個同構為τ:L→L),但這個同構不是“自然”的.即,若L1與L2間有一個同構α:L1→L2,“*”誘導出L2到L1的一個同構為α,但對L1中的元素x來說,τα(x)一般地並不等於ατ(x)。這就引起“自然性”的研究。艾倫伯格(Eilenberg,S.)與麥克萊恩(MacLane,S.)於1945年發表的論文《自然等價的一般理論》為範疇論的建立作出了奠基性的工作。
在某種意義上來說,範疇論提煉了數學(甚至其他學科)各分支的共性,是比集合論更高一個層次的數學公共語言與工具.它使數學各個領域的研究通過箭頭圖做了一致化與簡單化的處理,更加顯示其本質上的東西,同時使許多數學系統的性質通過圖的泛性質得到了深刻的刻畫。戈德門特(Godement,R.)於1958年將範疇論套用到拓撲學,埃雷斯曼(Ehresmann,C.)於1958年將範疇論套用到微分幾何,格羅騰迪克(Grothendieck,A.)與迪厄多內(Dieudonné,J.)於1960年將範疇論套用到代數幾何.現在,範疇論在上述學科及同調代數、代數K理論、模論、環論等學科中都得到了成功的套用。套用範疇論時,關鍵是先搞清研究問題以什麼作對象,以什麼作態射(參見“範疇”).研究不同範疇之間的關係時,關鍵在於找到適當的函子。範疇論的核心是函子理論。艾倫伯格與麥克萊恩為了搞清某些同構(等價)的“自然”變換之精確含義,於1945年引入範疇與函子的概念去定義自然變換。現在,範疇論已滲透到現代數學的各個領域(甚至已套用到計算機科學等),成為現代數學的基礎。
概形
代數幾何的基本研究對象。它實際上就是一個局部同構於仿射概形的局部環空間。更精確地,概形(X,OX)是一個環空間,其拓撲空間X有一個開覆蓋{Xi}i∈I,使得(Xi,OX|Xi)同構於仿射概形Spec Γ(Xi,OX)(這樣的覆蓋稱為仿射開覆蓋)。概形間的態射就是局部環空間的態射。概形的範疇是局部環空間範疇的子範疇.若概形X有一個仿射開覆蓋{Xi},使得每個仿射概形都是諾特概形、既約概形、正規概形或正則概形,則相應地稱概形X是局部諾特的、既約的、正規的或正則的。這些性質都是概形的局部性質,就是說,只要存在一個仿射開覆蓋具有上述某種性質,這個概形就具有此性質,而且任意一個仿射開子概形都有此性質。若概形X的拓撲空間是連通空間或不可約空間(即它不能表成兩個不同真閉子集的並),則稱此概形為連通的或不可約的。
在研究概形的性質或有關的概念時,往往要考慮具有相同基礎的概形。帶有態射f:X→S的概形X稱為S概形.若S=Spec A是仿射概形,則S概形簡稱A概形。顯然任何概形都是Z概形。給出基變換態射S′→S後,可以得到一個S′概形XS′=X×SS′,稱為S概形X的基擴張。與S概形相關的概念稱為相對概念,以區別於與概形相關的絕對概念.S概形與態射f:X→S密切相關。不同性質的態射就給出了不同的S概形。例如,設f:X→S是一個態射,若對角浸入X→X×SX是閉態射,則稱f是分離態射;若存在S的一個仿射開覆蓋{Ui}={Spec Bi},使得每個f(Ui)都有一個有限仿射開覆蓋{Vij}={Spec Aij},並且Aij都是有限生成Bi代數,則稱f是有限型的;若f(Ui)=Spec Ai,Ai都是有限生成Bi模,則稱f是有限態射。有限態射是仿射態射。代數幾何中研究的S概形一般都是分離、有限型的。
