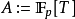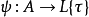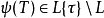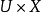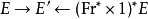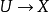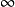德林費爾德模

在數學領域，德林費爾德模或橢圓模是一種特別的模，布於有限域上的代數曲線的坐標環上。粗略地說，德林費爾德模是復橢圓曲線的復乘法理論之函式域版本。

基本介紹

• 中文名：德林費爾德模
• 分布：有限域上的代數曲線的坐標環上
• 學科：數學
• 領域：數學

介紹

在數學領域，德林費爾德模或橢圓模是一種特別的模，布於有限域上的代數曲線的坐標環上。粗略地說，德林費爾德模是復橢圓曲線的復乘法理論之函式域版本。

俄文單詞штука（英語拼音：shtuka或chtouca，源於德文的Stück，意指物件或東西），又稱F-層，是德林費爾德模的一種延伸，由曲線上的向量叢和其它關乎弗羅貝尼烏斯映射的資料組成。

弗拉基米爾·德林費爾德在1973年發明了德林費爾德模，隨後推廣到 штука，以證明函式域上的郎蘭茲猜想。洛朗·拉福格藉由研究n秩 штука的模疊與跡公式，在2002年證出 的情形。

定義

加性多項式環

設 L 為特徵 p>0的域。定義其上的非交換多項式環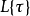

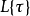
• a₀+a₁τ+a₂τ+...

乘法由下述條件確定

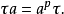
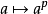元素可構想為弗羅貝尼烏斯映射。事實上，L是左 -模，其中 L 以乘法作用而以 映射。環 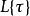也可以看作是如下多項式的集合

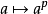
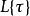
這類多項式滿足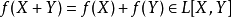，故稱加性多項式；此環的乘法由多項式的合成給出，而非乘法，故非交換。

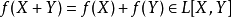
形式定義

今設A為交換環，L上的德林費爾德A-模定義為環同態，使得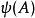不包含於L；此條件意在排除一些平凡例子。環A通常取作某條有限域上的仿射曲線的坐標環。

可視為加法群 (L,+) 的自同態，而德林費爾德A-模可視為A在 (L,+) 上的作用。

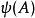
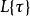
例子

置，對應到虧格為一的仿射代數曲線。德林費爾德模僅依賴於像。此時德林費爾德模可等同於。對於虧格更高的曲線，德林費爾德模會更複雜。

承上，Carlitz 模是由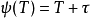，L為含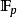的完備代數封閉域給出的德林費爾德模。此模首先由 Leonard Carlitz 在1935年展開研究。

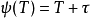
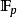
延伸

設X是有限域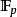上的代數曲線。對概形或疊U，其上的秩r（右）штука由下列資料定義：

上的秩r局部自由層E,E'及單射，其餘核的支撐集包括於某態射的圖（稱為該 штука 的零點與極點，記為0與 ），且在支撐集上是秩1局部自由層。在此Fr表U上的弗羅貝尼烏斯態射。

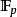
左 штука 的定義類似，但態射的方向反轉；若極點與零點集互斥，則實際上無分左右。

德林費爾德模可在某種意義下視作特別的 штука（自定義觀之，這絕非明顯）。

套用

簡言之，函式域上的郎蘭茲猜想是關於的尖點自守表示及某個伽羅瓦群的表示之間的對應。德林費爾德利用 штука 證明n=2的情形。此猜想的難處在於構造滿足特定性質的伽羅瓦表示，德林費爾德的高處在於從某個秩2штука 的模空間的-進上同調入手，找出相應的伽羅瓦表示。

德林費爾德認為此法可延伸至的情形。拉福格最後克服了其中的大量技術困難，完成證明。