跡公式(trace formula)亦稱塞爾貝格跡公式,波松求和公式的推廣.它是由塞爾貝格(( Sel- berg , A.)於1956年提出的。
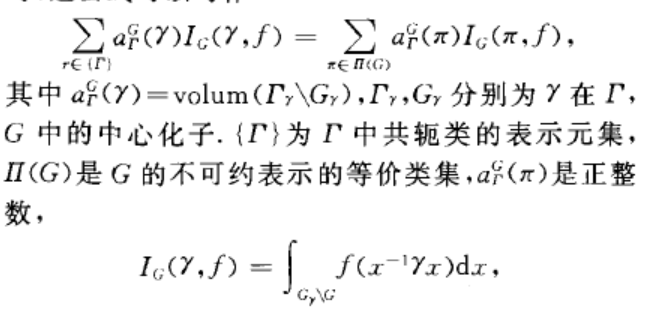
跡公式(trace formula)亦稱塞爾貝格跡公式,波松求和公式的推廣.它是由塞爾貝格(( Sel- berg , A.)於1956年提出的。
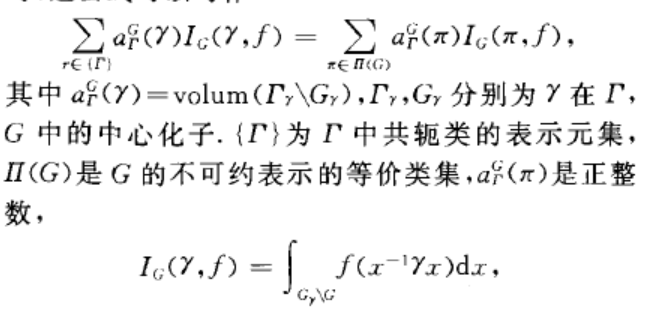
跡公式(trace formula)亦稱塞爾貝格跡公式,波松求和公式的推廣.它是由塞爾貝格(( Sel- berg , A.)於1956年提出的。...
塞爾伯格跡公式是數學中非交換調和分析的重要定理之一。此公式表達了齊性空間 G/ Γ 的函式空間上某類運算元的跡數,其中G是李群而Γ是其離散子群。又數學家...
計算公式是人們在研究自然界物與物之間時發現的一些聯繫,並通過一定的方式表達出來的一種表達方法。是表征自然界不同事物之數量之間的或等或不等的聯繫,它確切的...
帕塞瓦爾公式(Parseval formula)是經典帕塞瓦爾公式的推廣。在特殊情況f=g時,帕塞瓦爾公式就是普朗歇爾公式。...
數學公式是人們在研究自然界物與物之間時發現的一些聯繫,並通過一定的方式表達出來的一種表達方法。是表征自然界不同事物之數量之間的或等或不等的聯繫,它確切的...
1、通用格式,用數學符號表示,各個量之間的一定關係(如定律或定理)的式子,能普遍套用於同類事物的方式方法。2、公式,在數學、物理學、化學、生物學等自然科學中用...
德雷克公式 又叫德雷克方程(Drake equation,又稱薩根公式(Sagan equation)或格林班克公式(Green Bank equation)),後又稱“綠岸公式”。由美國天文學家法蘭克·德雷克...
《Jacobi形式的跡公式》是一部基礎數學類型的學術性論文,作者是李雲峰。...... 《Jacobi形式的跡公式》是一部基礎數學類型的學術性論文,作者是李雲峰。...
弦長公式,在這裡指直線與圓錐曲線相交所得弦長d的公式。PS:圓錐曲線, 是數學、幾何學中通過平切圓錐(嚴格為一個正圓錐面和一個平面完整相切)得到的一些曲線,如:...
《英雄伝說零の軌跡碧の軌跡公式設定資料集 クロスベルアーカイブ》是2012年4月27日アスキー・メディアワークス出版的圖書,作者是ファルコム。...
作為大數學家,塞爾伯格對現代數學還有兩大貢獻,實際上開拓兩個至今仍在發展的新分支:一是跡公式及相關的調和分析,另一是離散子群。由於這些貢獻,塞爾伯格成為美國...
研究了次正常運算元組的一個很有用的數學工具“精刻函式”, 並建立了關於具跡類自交換子的次正常運算元組的跡公式。對具有限秩自交換子的次正常運算元進行了深入的...
《泛函分析》還涉及了對於計算拓撲不變數十分重要的運算元的指標、強有力的分析工具Lidskii跡公式、Fredholm行列式及其推廣,以及源自於物理的散射理論及其他特殊論題。...
1 猜想的最早由來 2 1950年代與塞爾伯格跡公式 3 1970年代與隨機矩陣 4 與量子力學的可能聯繫 希爾伯特-波利亞猜想猜想的最早由來 編輯 在...
17. 9 泊松求和公式與塞爾伯格跡公式 // 308第十八章 朗蘭茲猜想,朗蘭茲綱領 // 312附錄附錄A 理想的產生歷史與計算 // 325...
解答一:依題意,記B(-1,b),(b∈R),則直線OA和OB的方程分別為y=0或y=-bx,設點C(x,y),則有0≤x據點到直線的距離公式可得. ①...
