上同調函子是一種重要的函子,指由上復形的範疇到模範疇的函子。範疇A-Cocomp,它的對象是環 A 上所有上復形,態射是復形的平移,把這個範疇稱為上復形的範疇,它是一個阿貝爾範疇。
基本介紹
- 中文名:上同調函子
- 外文名:cohomology functor
- 適用範圍:數理科學
簡介


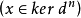
同調函子
上同調模

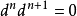
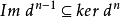
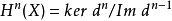

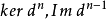

上同調函子是一種重要的函子,指由上復形的範疇到模範疇的函子。範疇A-Cocomp,它的對象是環 A 上所有上復形,態射是復形的平移,把這個範疇稱為上復形的範疇,它是一個阿貝爾範疇。


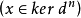

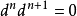
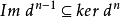
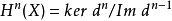

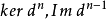

上同調函子是一種重要的函子,指由上復形的範疇到模範疇的函子。範疇A-Cocomp,它的對象是環 A 上所有上復形,態射是復形的平移,把這個範疇稱為上復形的...
數學中,霍赫希爾德同調(Hochschild homology)是環上結合代數的同調論。對某些函子也有一個霍赫希爾德同調。這是以德國數學家格哈德·霍赫希爾德(Gerhard Hochschild)冠名...
上同調模(cohomology modules)是一種重要的模。指由上復形給出的模。設:...2. 張亮. Weakly cofinite模及其局部上同調模的Ext函子的弱Laskerian性[J]....
《量子Schubert函子以及量子線性群的上同調》是胡峻的博士論文,由其導師王建磐教授指導完成。...
在範疇論中,函子(functor)是範疇間的一類映射,通俗地說,是範疇間的同態。...... 在範疇論中,函子(functor)是範疇間的...(如基本群、同調群或上同調群)的代數...
在同調代數中,阿貝爾範疇間的某類函子可以“求導”,以獲得相應的導出函子。此概念可以融貫數學中許多領域裡的具體構造。導出函子包括左導出函子和右導出函子。...
加性函子(additive functor)是範疇論與同調代數中常用的一類函子,即保持態射加法的函子,它只對加性範疇才有意義。設F為加性範疇C到加性範疇C′的函子,若對...
同調代數(homologicai algebra)是代數學的一個重要分支,主要研究在代數對象的各種範疇(如給定環上的模、層等)上的導出函子,第二次世界大戰後形成的新的數學分支,...
《同調代數導論》主要介紹證明Serre猜想的一些思想方法;第5章,群的擴張,初步介紹研究群結構的同調方法;第6章,同調論,主要介紹一般的同調概念和導出函子概念,及其粘...
1.3反變函子 1.4簡單的推論 2鏈復形與鏈映射 2.1鏈復形及其同調群 2.2鏈映射及其誘導同態 2.3鏈同倫 3奇異同調群 3.1奇異單形 3.2奇異鏈復形與奇異...
在同調代數中,內射對象與投射對象是內射模與投射模在阿貝爾範疇中的推廣,二者的定義相對偶。以下固定一個阿貝爾範疇。若對象 使得函子 為正合函子,則稱 為投射...
王建磐教授在代數群表示的科學研究和研究生培養方面努力工作,成為此方向的國內領軍人物,他在Weyl模張量積的Weyl模濾過的存在性、generic上同調的函子解釋、平移與...
