基本介紹
- 中文名:忠實函子
- 外文名:faithful functor
- 別稱:信守函子
- 相關概念:完全函子,恆等函子,具體範疇等
- 所屬學科:數學
基本介紹
定義
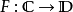

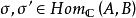

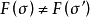
完滿函子與忠實函子







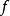

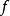





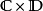

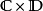



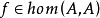






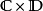

相關概念
恆等函子
具體範疇













範疇生成子
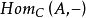

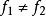


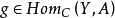
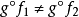

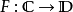

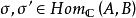

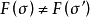







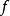






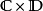

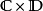



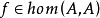






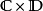









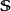



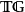


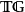
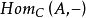

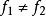


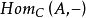
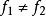
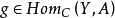
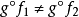
忠實函子(faithful functor)亦稱信守函子,是全函子的對偶概念。設F:C→D為函子,若τ,σ∈HomC(A,B),τ≠σ,必F(τ)≠F(σ),則稱F為C到D的忠實函...
在範疇論中,函子(functor)是範疇間的一類映射,通俗地說,是範疇間的同態。...... 為滿射的函子。5)完全忠實函子:既完全且忠實的函子稱為完全忠實函子。 是完...
全忠實函子(full faithful functor)一種特殊的函子.它是關於態射變元為滿單射的函子.若函子F是全函子也是忠實函子,則稱F為全忠實函子. ...
嵌入函子(embedding functor)一類特殊的忠實函子.關於態射及對象都是單射的函子,設F為函子,若aEHom}=(A,B),必F =F (Q),則稱F為子函子,即變不同對象...
給定一個 的子範疇 ,其包含函子 在物件上是忠實且單射的。此函子為完全的若且唯若 為一完全子範疇。一個函子 被稱之為是一個內嵌若其為:...
。兩個模範疇C,D等價的充分必要條件是,存在全忠實函子 ,並且對任意 ,總有 ,使得 同構於 。模範疇的等價理論是模論的一個重要組成部分,森田紀一(Morita Kiiti...
存在從FG到ID與從IC到GF的自然同構,分別叫做余單位與單位。 F是G的一個左伴隨且兩個函子都完全且忠實。 F是G的一個右伴隨且兩個函子都完全且忠實。...
此時,也稱環A與B是森田紀一相似的,記為B}A.兩個模範疇留,少等價的充分必要條件是,存在全忠實函子F;}0}},並且對任意M' E obi,總有ME ob}0,使得F(M)...
範疇生成子(generator of a category)範疇的一個特殊對象.範疇}0中使Homc (A,一)為忠實函子的對象A稱為它的一個生成子.換句話說,對任意的留中對象X,Y,若...
