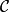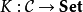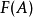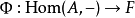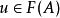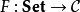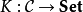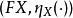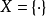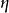可表函子

可表函子是在數學中範疇論里的概念，指從任意範疇到集合範疇的一種特殊函子。

這種函子將抽象的範疇表達成人們熟知的結構（即集合與函式），從而使得對集合範疇的了解可以儘可能套用到其它環境中。

基本介紹

• 中文名：可表函子
• 外文名：Table functor
• 概述：從任意範疇到集合範疇的特殊函子
• 學科：數理科學

定義

設C 為局部小範疇，並記集合範疇為Set 。對 C 中的每個對象 A以Hom (A,-)指代將對象X 映到集合Hom (A,X) 的Hom函子。

函子是可表的當存在某個C中的對象A使得 F自然同構於Hom (A,X)。而滿足

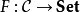
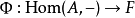
為自然同構的對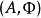 則稱為 F的一個表示。

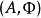
從C到Set 的反變函子G不過是（協變）函子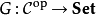，常被稱作預層。與協變的情況相似，預層是可表的當它自然同構與某個反變的Hom函子 Hom (-,A)，其中 A是C 中的某個對象。

泛元素

根據米田引理，從Hom (-,A)到 F 的自然變換與集合一一對應。給定自然變換，與之對應的元素 由

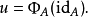
給出。反之，給定元素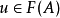，可以如下定義自然變換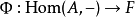

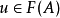
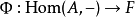
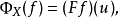
其中 f 是Hom (A,X)中的任意元素。為了得到 F 的表示，我們需要確定 u誘導的自然變換何時會是同構。這引導出如下定義：

函子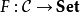的泛元素是由C中的對象 A與 F(A) 中的元素 u 組成的一對 (A,u)，使得對於任意滿足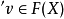的對 (X,v)，都存在唯一映射 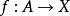使得。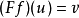

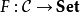
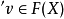
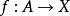
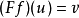
泛元素還可看作從單點集合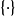到函子{ F}的泛態射，又或者看作{ F}的元素範疇中的始對象。

性質

唯一性

函子的表示在同構的意義下唯一。

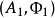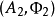換言之，如果與 表示同一個函子，那么存在唯一的同構 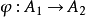使得

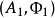
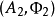
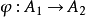
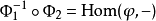
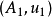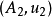用泛元素的語言表述如下：如果與 表示同一個函子，那么存在唯一的同構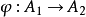使得

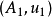
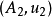
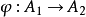
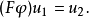
保極限性

可表函子自然同構於Hom函子，因而享有許多後者的性質。尤其值得注意的是，（協變）可表函子保持所有極限。由此可得，未能保持某些極限的函子都不是可表的。

相似地，反變可表函子把余極限映到極限。

左伴隨

如果函子 帶有左伴隨，那么它就可由 表示；這裡是某個單元素集合，而是伴隨的單位。

反之，如果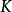由對(A,u)表示，且 A 的任意上冪在 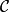中都存在，那么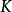擁有左伴隨F，後者將任意集合 I映到 A 的I 次上冪。

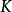
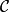
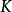
所以，如果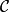是帶所有上冪的範疇，則函子 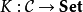是可表的若且唯若它擁有左伴隨。