始對象(initial object)是範疇論的基本概念之一,指在範疇論中起著特殊作用的一類對象,是終對象的對偶概念,它們都是零對象的推廣。設C為範疇,A∈C,若對一切B∈C,Hom(A,B)都只有一個元素,則稱A為範疇C的始對象,C的任何兩個始對象必是等價(同構)的。例如,阿貝爾群範疇的始對象為0(零群)。
基本介紹
- 中文名:始對象
- 外文名:initial object
- 所屬學科:數學
- 所屬問題:範疇論的基本概念之一
- 相關概念:終對象、零對象等
定義,相關定理,舉例分析,
定義
(2) 設 是範疇,
是範疇, ,若對於
,若對於 ,
, 都是僅含單獨一個元素的集,則稱
都是僅含單獨一個元素的集,則稱 是
是 的終對象(terminalobject)。
的終對象(terminalobject)。






(3) 若 既是始對象又是終對象,則稱
既是始對象又是終對象,則稱 是
是 的一個零對象(null object)。
的一個零對象(null object)。



相關定理
定理1 (1)若 是範疇
是範疇 的一個終(始)[零]對象,
的一個終(始)[零]對象, 是範疇
是範疇 的一個終(始)[零]對象。
的一個終(始)[零]對象。




(2) 若範疇 有始(終)[零]對象,則各個始(終)[零]對象必是等價對象,因而從同構的觀點看它們都是唯一的。
有始(終)[零]對象,則各個始(終)[零]對象必是等價對象,因而從同構的觀點看它們都是唯一的。

定理2 在一個範疇 中的始對象與終對象是對偶的,從而零對象是自對偶的。
中的始對象與終對象是對偶的,從而零對象是自對偶的。

證明:設 表示範疇
表示範疇 中始對象的定義。於是
中始對象的定義。於是



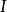





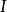




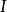




命題3 設 是範疇,若
是範疇,若 中的對象
中的對象 都是始(或終)對象,則
都是始(或終)對象,則 。
。




證明: 若 中的對象
中的對象 都是始對象,則
都是始對象,則 都是單元集。設
都是單元集。設 ,於是
,於是 ,注意
,注意 ,並且
,並且 是始對象,所以
是始對象,所以 。同理
。同理 。綜上所證,可知
。綜上所證,可知 。
。










舉例分析
例1在集範疇Set中空集 是始對象但不是終對象,單元集是終對象但不是始對象;每個單元素集如
是始對象但不是終對象,單元集是終對象但不是始對象;每個單元素集如 是一個終對象而不是始對象,可以證明,它沒有零對象。
是一個終對象而不是始對象,可以證明,它沒有零對象。


例2 在範疇Grp和Ab中僅含一個元素的群 (當群的複合運算是乘法時是
(當群的複合運算是乘法時是 )既是它們的始對象也是它們的終對象,因而是它們的零對象。在範疇Grp中,平凡群是零對象。
)既是它們的始對象也是它們的終對象,因而是它們的零對象。在範疇Grp中,平凡群是零對象。







