函子自然變換是處理函子之間關係的一個重要概念,由它可得出有用的可換圖。
基本介紹
- 中文名:函子自然變換
- 外文名:natural transformation of functors
- 適用範圍:數理科學
簡介
 圖1.
圖1.自然等價
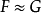
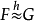
函子自然變換是處理函子之間關係的一個重要概念,由它可得出有用的可換圖。
 圖1.
圖1.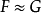
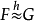
函子自然變換是處理函子之間關係的一個重要概念,由它可得出有用的可換圖。...... 函子自然變換是處理函子之間關係的一個重要概念,由它可得出有用的可換圖。...
可表函子是在數學中範疇論里的概念,指從任意範疇到集合範疇的一種特殊函子。...給出。反之,給定元素 ,可以如下定義自然變換其中f 是Hom (A,X)中的任意...
範疇論的核心是函子理論。艾倫伯格與麥克萊恩為了搞清某些同構(等價)的“自然”變換之精確含義,於1945年引入範疇與函子的概念去定義自然變換。現在,範疇論已滲透到...
範疇論的核心是函子理論。艾倫伯格與麥克萊恩為了搞清某些同構(等價)的“自然”變換之精確含義,於1945年引入範疇與函子的概念去定義自然變換。現在,範疇論已滲透到...
與協變的情況相似,預層是可表的當它自然同構與某個反變的Hom函子 ,其中 是 中的某個對象。表示函子泛元素 編輯 根據米田引理,從 到 的自然變換與集合 ...
艾倫伯格與麥克萊恩為了搞清某些同構(等價)的“自然”變換之精確含義,於1945年引入範疇與函子的概念去定義自然變換。現在,範疇論已滲透到現代數學的各個領域(甚至已...
對於左導出函子,相應的長正合序列形如:此外,這些長正合序列在下述意義下是“自然”的:短正合列之間的態射導出長正合序列間的態射。 函子間的自然變換導出長...
在範疇論中,函子(functor)是範疇間的一類映射,通俗地說,是範疇間的同態。...... 。函子 是一個自然的例子,它對第一個...中的交換圖變換成中的一個交換圖;2...
範疇,函子和自然變換是由塞繆爾·艾倫伯格和桑德斯·麥克蘭恩在1945年引進的。這些概念最初出現在拓撲學,尤其是代數拓撲學裡,在同態(具有幾何直觀)轉化成同調論(...
研究不同範疇之間的關係時,關鍵在於找到適當的函子。範疇論的核心是函子理論。艾倫伯格與麥克萊恩為了搞清某些同構(等價)的“自然”變換之精確含義,於1945年引入範疇...
在光滑流形範疇中,態射是光滑函式而同構稱為微分同胚。 函子可以視為小範疇的範疇中的態射。 在函子範疇中,態射是自然變換。參考...
範疇論的核心是函子理論。艾倫伯格與麥克萊恩為了搞清某些同構(等價)的“自然”變換之精確含義,於1945年引入範疇與函子的概念去定義自然變換。現在,範疇論已滲透到...
主要內容包括6章:第1章著重介紹範疇的基本定義及其運算,第2章討論範疇中的特殊態射與特殊對象,第3章討論範疇中的各類極限,第4章討論函子與自然變換,第5章討論...
範疇論的核心是函子理論。艾倫伯格與麥克萊恩為了搞清某些同構(等價)的“自然”變換之精確含義,於1945年引入範疇與函子的概念去定義自然變換。現在,範疇論已滲透到...
研究不同範疇之間的關係時,關鍵在於找到適當的函子。範疇論的核心是函子理論。艾倫伯格與麥克萊恩為了搞清某些同構(等價)的“自然”變換之精確含義,於1945年引入範疇...
紹了範疇論的主要內容:範疇、函子、自然變換、積與和、極限和余極限、伴隨、笛卡兒封閉的範疇和素描等,並通過很多例子.介紹了範疇論在程式設計語...
在套用上,我們常常需要長正合列的“函子性”或曰“自然性”(就自然變換意義言之);各種建構的函子性也是同調代數的基本哲學。此函子性可由蛇引理的函子性導出...
一般來講,所有代數幾何的構造都是函子式的:概念範疇, 函子和自然變換起源於此。基本群,同調和上同調群不僅是兩個拓撲空間同胚時的不變數;而且空間的連續映射可以...
么半函子為二張量範疇(么半範疇)間、保存張量積結構之函子;么半態射為二么半函子間之態射(自然變換 (natural transformations))。 一般么半群之概念可推廣成么...
行列式映射det也是函子K0和Pic間的自然變換,即g:R→S為環同態時,[1] 行列式映射環論 編輯 抽象代數學的主要分支之一。它是具有兩個運算的代數系。在非空集合...
除了子群、正規子群及群同態的基本定理外,還介紹了有限群的西洛定理和可解群...§6.2 函子與自然變換 §6.3 可加範疇 §6.4 範疇等價 §6.5 函子的表示...
是實數。借著這些對偶性,下節描述的傅立葉變換將符應於 上的古典版本對偶...定理:對偶函子是一個範疇等價。定理:對偶函子的二次疊代自然同構於LCA上的恆等...
預層間的態射被定義為函子間的自然變換,這使得C上所有預層的蒐集構成了一個範疇 。到 的函子常被稱為Profunctor。預層性質 編輯 ...
對範疇的系統研究起始於S.Eilenberg和S.MacLane在代數拓撲學中的工作,他們在1945年提出範疇、函子和自然變換等基本概念,其後,在1958年,D.Ken明確地定義並研究了...
