反對稱化運算元

反對稱化運算元（anti-symmetrization operator）是作用於反對稱張量上的運算元。

基本介紹

• 中文名：反對稱化運算元
• 外文名：anti-symmetrization operator
• 適用範圍：數理科學

簡介

反對稱化運算元是作用於反對稱張量上的運算元。

對任意的x∈T^r(V)，令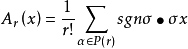，它稱為r階反變張量的反對稱化運算元。

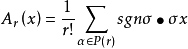
性質

用P^r(V)表示全體對稱的r階反變張量的集合，用Λ^r(V)表示全體反對稱的r階反變張量的集合。不難驗證有性質：S_r∘S_r=S_r，A_r∘A_r=A_r，且P^r(V)=S_r(T^r(V))，Λ^r(V)=A_r(T^r(V))。

反對稱張量

第一個張量對它的前兩個指標是對稱的，而第二個張量對前三個指標是對稱的。若有這樣的張量，它的兩個反變指標或共變指標互換時，張量的分量值改變符號而大小不變，則該張量稱為反對稱或斜對稱的。

運算元

運算元是一個函式空間到函式空間上的映射O：X→X。廣義上的運算元可以推廣到任何空間，如內積空間等。

廣義的講，對任何函式進行某一項操作都可以認為是一個運算元，甚至包括求冪次，開方都可以認為是一個運算元，只是有的運算元我們用了一個符號來代替他所要進行的運算。