模糊化運算元(operator for fuzziness)是一種運算元，是改變單詞的模糊程度的一種運算元。它是這樣一個詞，放在某個單詞前面可使這個單詞的意義更加模糊，比如“大概”、“近似”等，一般可用一個模糊相似關係(即自反、對稱的模糊關係)來表示，若A是論域X上的一個單詞，E為X上的模糊化運算元，由(EA)(x)=(E°A)(x)可得到更加模糊化的單詞。
基本介紹
- 中文名：模糊化運算元
- 外文名：operator for fuzziness
- 所屬學科：數學（模糊數學）
- 簡介：改變單詞的模糊程度的一種運算元
基本介紹,例題解析,
基本介紹
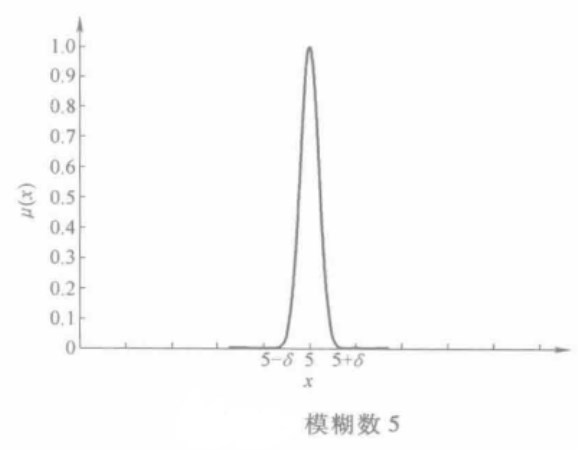
模糊化運算元用來使語言中某些具有清晰概念的單詞或詞組的詞義模糊化，或者是將原來已經模糊概念的詞義更加模糊化，如“大概”、“近似於”、“大約”等。如果模糊化運算元對數字進行作用，就意味著把精確數轉化為模糊數。例如數字“5”是一個精確數，而如果將模糊化運算元“F”作用於“5”，則這個精確數就變成“F(5)”這一模糊數。若模糊化運算元“F”是“大約”，則“F(5)”就是“大約5”這樣一個模糊數。在模糊控制中，實際系統的輸入採樣值一般總是精確量，要利用模糊邏輯推理方法，就必須首先把精確量進行模糊化，而模糊化過程實質上是使用模糊化運算元來實現的。所以，引入模糊化運算元是非常重要的。用數學語言，模糊化運算元的集合可以表示如下：
設模糊化之前的集合為A，模糊化運算元為F，則模糊化變換可表示為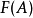
，並且它們的隸屬度函式關係滿足
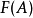
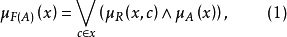
例題解析
【例1】 設論域X上的清晰集
為
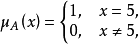
解 根據式(1)可知
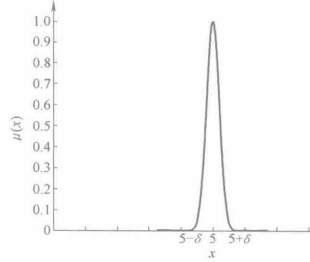圖1 模糊數5