第一個張量對它的前兩個指標是對稱的,而第二個張量對前三個指標是對稱的。若有這樣的張量,它的兩個反變指標或共變指標互換時,張量的分量值改變符號而大小不變,則該張量稱為反對稱或斜對稱的。
基本介紹
- 中文名:反對稱張量
- 外文名:antisymmetric tensor
- 定義:張量的分量值改變符號而大小不變
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:張量
- 類型:數理科學領域術語
概念









基本原理








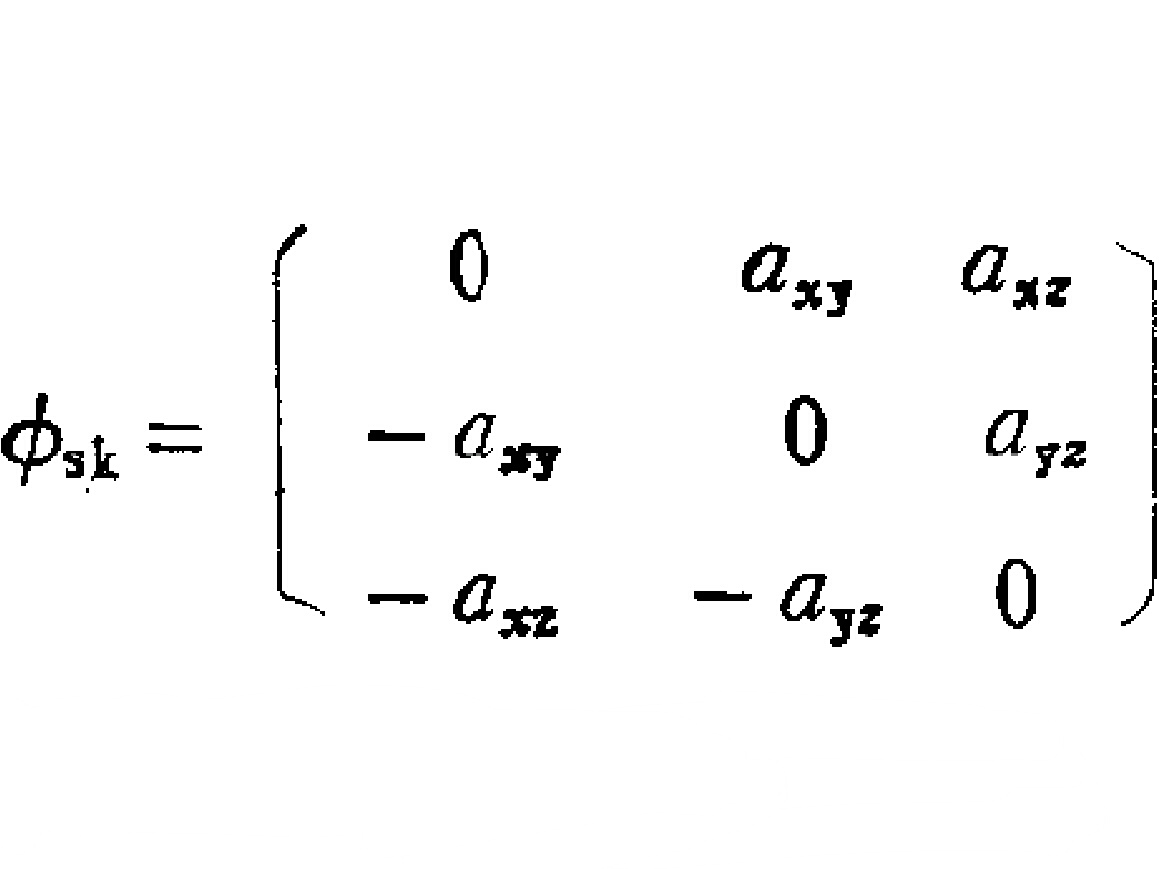




第一個張量對它的前兩個指標是對稱的,而第二個張量對前三個指標是對稱的。若有這樣的張量,它的兩個反變指標或共變指標互換時,張量的分量值改變符號而大小不變,則該張量稱為反對稱或斜對稱的。

















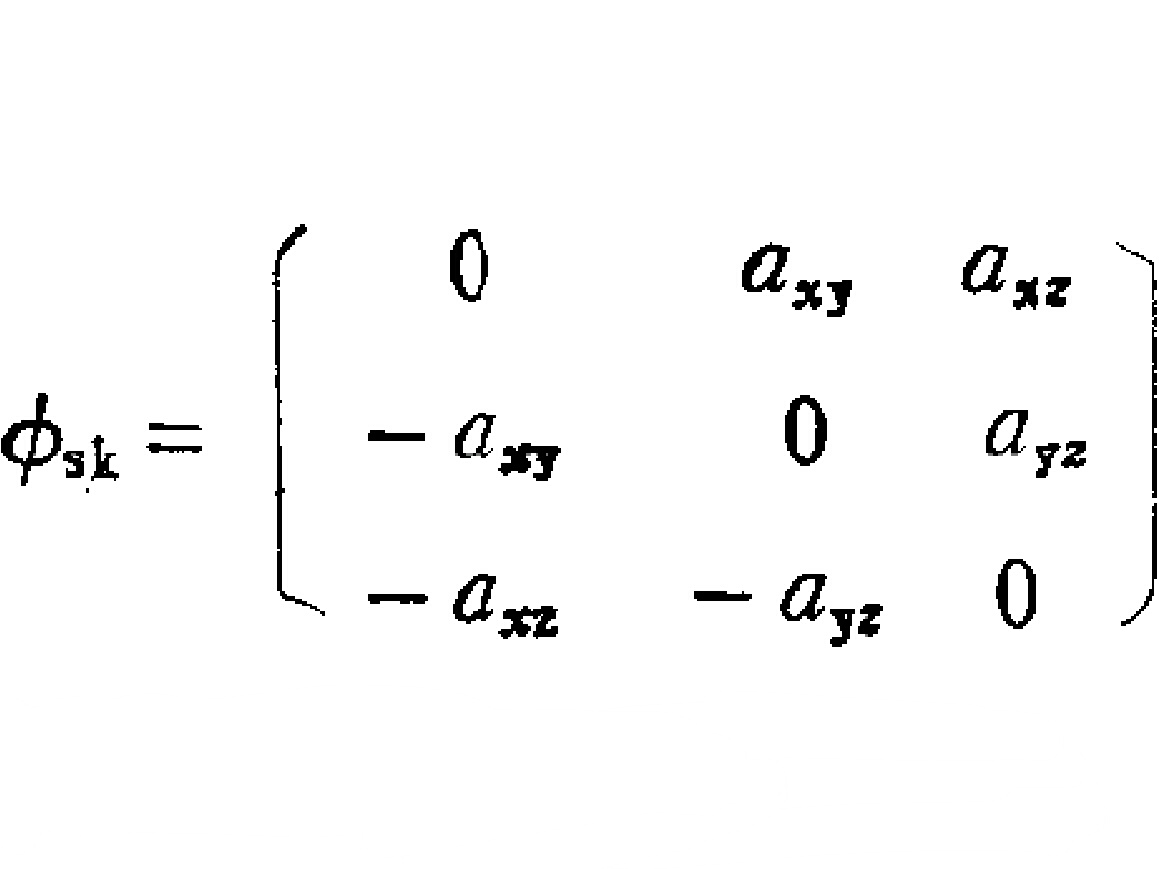



對稱化運算元(symmetrization operator)是作用於反對稱張量上的運算元。張量是向量概念的綜合,可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力聯繫起來。張量計算最初的發展是與微分幾何相聯繫的,也是愛因斯坦在系統...
2.1.2二階張量的轉置,對稱、反對稱張量及其所對應的矩陣46 2.1.3二階張量的行列式47 2.1.4二階張量的代數運算與矩陣的代數運算47 2.2正則與退化的二階張量49 2.2.1關於映射的幾個定理49 2.2.2正則與退化49 2.3二階...
,都有σx=sgn σ·x,其中sgn σ表示置換σ的符號,即:則稱x是反對稱r階反變張量。設x∈T(V),則x是對稱張量的充分必要條件是它的分量關於各指標是對稱的。x是反對稱張量的充分必要條件是它的分量關於各指標是反對稱的。
§7.1 三重系變換下張量的定義 §7.2 三重系下張量的加法、減法、張量積和數乘 §7.3 張量的縮並 §7.4 張量的內積運算 §7.5 張量的商法則 §7.6 相伴張量、對稱張量、反對稱張量 §7.7 從張量的運算看矢量的矢量...
對稱張量是各分量關於指標對稱的張量,表示r階反變張量全體。x是對稱張量的充分必要條件是它的分量關於各指標是對稱的,x是反對稱張量的充分必要條件是它的分量關於各指標是反對稱的。定義 如果一個p次反變張量在自然同構 下所對應p...
另一類是贗矢量(如磁場強度、磁感應強度、磁化強度、動量矩等),形式上為矢量,其實是反對稱的二階張量,稱為軸矢量。其變換公式為,式中||為正交變換矩陣的行列式,在純轉動時為1,中心反演或轉動-反演時為-1。根據物理方程即可...
9.3Matlab的張量運算 9.4Mathematica的張量運算 習題 附錄A示範例題 張量概念 逆變矢量、協變矢量和張量 克羅內克符號δ 張量的基本運算 對稱張量和反對稱張量 矩陣 線元和度量張量 相伴張量 克里斯托費爾符號 測地線 協變導數 張量形式...
9.3Matlab的張量運算 9.4Mathematica的張量運算 習題 附錄A示範例題 張量概念 逆變矢量、協變矢量和張量 克羅內克符號δ 張量的基本運算 對稱張量和反對稱張量 矩陣 線元和度量張量 相伴張量 克里斯托費爾符號 測地線 協變導數 張量形式...
格拉斯曼空間亦稱反對稱張量空間。是一個最常見的張量對稱類,即當G=Sₘ,χ=ε(符號特徵標)時的張量對稱類。通常寫為:可合元素則寫為:T(Sₘ,ε)v=v=v₁∧v₂∧…∧vₘ,又稱為v₁,v₂,…,vₘ的外積。
5.3Descartes張量的運算 5.3.1張量的線性相加 5.3.2張量的相等 5.3.3零張量 5.3.4單位張量 5.3.5張量的縮並 5.3.6張量的乘法 5.3.7張量的縮乘 5.3.8張量的導數 5.3.9張量方程 5.4對稱和反對稱張量 5.4.1張量...
1.6.3 對稱張量的另外一種分解 37 1.6.4 對稱張量的正定性 39 1.7 反對稱張量 41 1.8 正交張量 44 1.8.1 正交張量的定義 44 1.8.2 非正常正交張量 45 1.8.3 正常正交張量使用反對稱張量的表示 48 1.8.4 正交...
2.2 張量與張量代數 49 2.2.1 張量及其表示 49 2.2.2 張量積和張量代數 50 2.2.3 張量的縮並運算 53 2.2.4 度量張量、指標的提升和下降 54 2.3 對稱張量和反對稱張量 55 2.3.1 對稱與反對稱張量 ...
1.6 張量的基本概念和表示 13 1.6.1 張量的基本概念 14 1.6.2 參考三維空間中協變與逆變基向量的張量表示 14 1.6.3 對稱張量和反對稱張量 14 1.7 標準正交坐標系下張量的坐標變換與剛體旋轉 15 1.7.1 向量的坐標變換 ...
伸縮子(dilaton):是決定弦偶合的正能量超光速迅子 伸縮子(dilaton):是決定弦偶合的粒子,早期弦論中,有反對稱張量場,此張量場相當於反引力,而對稱張量即相當於引力,伸縮子即具有這2種力,上述反引力是類似迅子的超光速反引力,而超...
張量上的拉普拉斯運算元 利用與列維-奇維塔聯絡相伴的共變導數,拉普拉斯–貝爾特拉米運算元可推廣到偽黎曼流形上任意張量。這個推廣的運算元可以作用在反對稱張量上。但所得的運算元與拉普拉斯–德拉姆運算元給出的不同:兩者通過外森比克恆等式相關。...
1. 標量,向量與張量459 2. 場459 3. 標量場的梯度460 4. 向量場的散度461 5. 向量場的旋度461 6. 高斯公式462 7. 張量的表示法,二階張量463 8. 單位張量δ和置換張量εijk467 9. 二階對稱張量與二階反對稱張量468 10....
第5章 二階張量 5.1 二階張量和不變數 5.2 特片值和特徵向量 5.3 Cayley-Hamilton定理 5.4 不變數間的關係 5.5 對稱張量 5.6 反對稱張量 5.7 極分解定理 思考題與習題 第6章 應變和應變速率 6.1 位移梯度 6.2 應變...
第五章 張量分析與黎曼幾何 5.1 流形上張量場的一般概念 5.2 張量場的簡單例子 5.2.1 例 5.2.2 張量的代數運算 5.2.3 反對稱張量 5.3 聯絡和共變微分 5.3.1 仿射聯絡的定義和性質 5.3.2 黎曼聯絡 5.4 ...
(B) 張量初步 1.13 張量的定義 1.14 張量的代數運算 1.15 張量識別定理 1.16 二階張量 1.17 二階反對稱張量的性質 1.18 二階對稱張量的性質 1.19 張量的微分運算 1.20 各向同性張量 習題二 第二章 流體力學的基本...
1.6.2 張量對稱、反對稱 1.7 階張量(仿射量)1.7.1 二階張量基本代數運算 1.7.2 階張量行列式 1.7.3 正則二階張量、二階張量的逆 .1.7.4 二階張量不變數(n=3)1.7.5 二階張量特徵值問題(n=3)第2章 拓撲結構 2...
由此,可將規範引力量子場論與愛因斯坦廣義相對論進行比較,從而得到幾何引力場方程:一組對應於愛因斯坦廣義相對論的引力場方程,由對稱的能動量張量支配;另一組引力場方程是超越愛因斯坦廣義相對論的引力場方程,由反對稱能動量張量支配。...
