完全對稱化子

完全對稱化子(completely symmetrizer)是張量空間上的一種投影運算元，有時也稱為對稱化子。多重線性代數的重要概念。定義有張映射的一種向量空間。具體定義有多種不同的形式。張量空間對於多重線性代數的重要性如同向量空間對於線性代數的重要性。

基本介紹

• 中文名：完全對稱化子
• 外文名：completely symmetrizer
• 別名：對稱化子
• 領域：數學
• 空間：張量空間
• 性質：投影運算元

概念

完全對稱化子是張量空間上的一種投影運算元。有時也稱為對稱化子。設E是特徵為0的域K上的向量空間，為E的p次張量冪，p≥2，若，S_p是p階對稱群，對任意σ∈S_p，σu=u，則u稱為對稱張量。若：

則π_s是的線性映射，稱為上的對稱化子。π_su稱為u的對稱部分。若中對稱張量所成的子空間為Y(E)，M(E)為{u-τu|u∈，τ∈s_p}生成的之子空間，則：

並且，

向量空間

設K為交換體。稱賦以由下列兩個給定法則所定義的代數結構的集合E為K上的向量空間：

——記為加法的合成法則，

——記為乘法的作用法則，即從K×E到E中的映射，

這兩個法則滿足下列條件：

a)賦以加法的集合E是交換群；

b) 對K的任一元素偶(α，β)，以及對E的任一元素x，α(βx)=(αβ)x；

c) 對E的任一向量x，1x=x，其中1表示體K的單位元素；

d)對K的任一元素偶(α，β)，以及對E的任一元素偶(x，y)，(α+β)x=αx+βx，α(x+y)=αx+αy。

當體K不再假定為交換的時，滿足上述條件的集合E稱為K上的左向量空間。

如果條件α(βx)=(αβ)x換為α(βx)=(βα)x，則稱E為K上的右向量空間。在這種情況下，E上的作用法則記為：

例如，設K為交換體，而E為只有一個記為0的元素的集合。E賦以兩個法則：(0，0)↦0，(α， 0)↦0則E為K上的向量空間。

張量空間

多重線性代數的重要概念。定義有張映射的一種向量空間。具體定義有多種不同的形式。例如，可定義為：設P是一個向量空間，若存在張映射：V₁×V₂×…×V_m→P使得〈Im〉=P，則稱P為V₁，V₂，…，V_m的帶有張映射的張量空間；或稱P為V₁，V₂，…，V_m的張量積空間；或簡稱P為V₁，V₂，…，V_m的張量積，記為：

張量空間對於多重線性代數的重要性如同向量空間對於線性代數的重要性。張量空間的維數是：

投影運算元

把任一元映到該元的正交投影的運算元。設M是希爾伯特空間H的閉線性子空間.對任意x∈H，必有分解x=x₁+x₂，x₁∈M，x₂∈M，定義運算元P如下：Px=x₁，即Px是x在M上的投影，稱運算元P為由H到M上的正交(或直交)投影運算元，簡稱投影(或射影)運算元。投影運算元P具有下列性質：P=P(冪等)；P有界(事實上有‖P‖=1)；對一切x，y∈H，(Px，y)=(x，Py)成立(自伴)。反之，H上有界自伴的冪等運算元必是投影運算元.正交投影運算元與H的閉線性子空間之間成一一對應。滿足PQ=0的兩個正交投影運算元P和Q稱為相互正交的，記為P⊥Q。

正交投影運算元是希爾伯特空間上特別重要的一類運算元。它是希爾伯特空間的很好的幾何特徵的反映，又是研究其他複雜運算元的工具。

張量

n維空間中的一個量，它具有nr個分量，用Ti1，_i2，…，_ir表示，它的每個分量都是坐標的函式；在坐標變換下，這些分量按照一定的規律作線性變換。r稱為張量的階。

張量是矢量及矩陣概念的推廣。標量是零階張量；向量是一階張量；矩陣是二階張量。三階張量(它的分量用Tijr表示)就像是一個“立體矩陣”。

在1900年，張量首先在彈性理論中使用。“張量”原來的含義是“張緊”與“張開”。

1892年起，里奇(C.G.Ricci，意，1853—1925)與列維·奇維塔(T.Levi-Civita，意，1873—1941)開始建立張量分析的理論，成為黎曼幾何與廣義相對論的一種工具。

為了簡便，在張量列式或計算時，常按求和約定將求和號略去。

對稱張量

各分量關於指標對稱的張量，即在正整數{1，2，…，r}的置換作用下不變的r階反變張量。記T(V)=V_r，o，它表示r階反變張量全體。P(r)表示{1，2，…，r}的置換群。設x∈T(V)，若對任意的σ∈P(r)，都有σx=x，則稱x是對稱的r階反變張量。若對任意的σ∈P(r)，都有σx=sgn σ·x，其中sgn σ表示置換σ的符號，即：

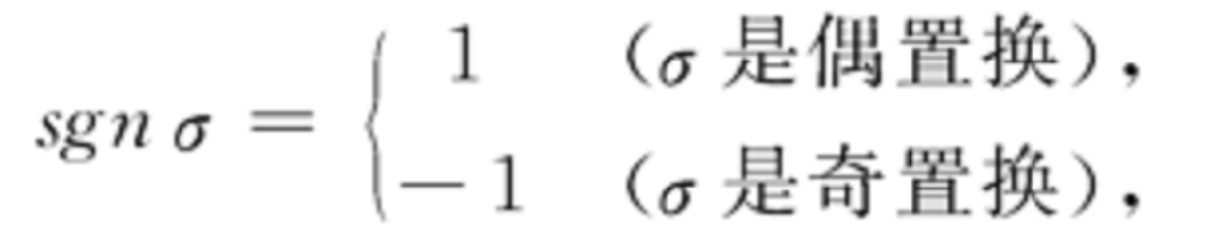
則稱x是反對稱r階反變張量。設x∈T(V)，則x是對稱張量的充分必要條件是它的分量關於各指標是對稱的。x是反對稱張量的充分必要條件是它的分量關於各指標是反對稱的。