基本介紹
- 中文名:閉線性子空間
- 外文名:closed linear subspace
- 適用範圍:數理科學
簡介
線性子空間
賦范空間
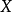

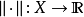
1)對
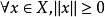
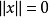

2)對
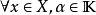
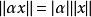
3)對

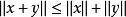
稱
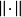
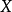
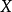

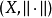
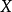
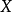

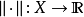
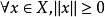
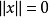

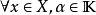
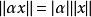

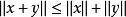
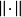
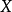
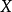

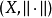
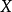
賦范空間中的按範數導出的距離還是閉的線性子空間稱為閉線性子空間。...... 閉線性子空間是一類子空間。賦范空間中的按範數導出的距離還是閉的線性子空間稱為閉...
特別,當M是H的閉線性子空間時,z=x-y必與M正交,即對於閉線性子空間M,分解x=y+z不僅惟一,而且z⊥y。這就是投影定理。其中,y稱為x在M中的投影(分量)。...
設T是希爾伯特空間H上的有界線性運算元,M是H的閉線性子空間,如果M和M⊥都是T的不變子空間,就稱M是T的約化子空間。...
稠定閉線性運算元是無界線性運算元理論中一類重要的運算元。稠定閉線性運算元稠密線性運算元 設X,Y為賦范線性空間,T是定義域為𝓓(T)⊂X,值域為𝓡(T)⊂Y的線性...
向量空間又稱線性空間,是線性代數的中心內容和基本概念之一。在解析幾何里引入向量概念後,使許多問題的處理變得更為簡潔和清晰,在此基礎上的進一步抽象化,形成了與...
在線性代數中,一個向量空間V被一個子空間N的商是將N“坍塌”為零得到的向量空間,所得的空間稱為商空間(quotient space),記作V/N(讀作V模N)。...
設X為線性賦范空間,X*為X的共軛空間,將X*的共軛空間(X*)*記為X**,稱X**為X的第二次共軛空間。設X為自反空間,則X*也是自反空間。拓撲空間是歐幾里得空間...
度量線性空間(metric linear space)是一類定義了距離的線性空間。設E是線性空間,又是度量空間,ρ是E上的距離,且E按ρ導出的拓撲成為拓撲線性空間,則稱E為度量...
設X,Y為賦范線性空間,T是線性運算元。如果𝓓(T)在X中是稠密的,則稱T是稠密線性運算元。...
4.2 線性運算元的性質、線性泛函的擴張4.3 基本集和全集4.4 空間C,L,c,l,m以及空間m的子空間中的有界線性泛函的一般形式4.5 空間C,L,c,l中的閉序列和完全...
線性空間又稱“向量空間”。它是元素(稱為向量)的集,其中有向量的“加法”、數與向量的“乘法”運算,且滿足加法交換律、結合律、分配律,還存在零元素,每個元素...
里斯引理(Riesz lemma)揭示閉子空間與單位球面上某點的距離性質的重要引理。...... 里斯引理揭示閉子空間與單位球面上某點的距離性質的重要引理。設Y是賦范線性空...
運算元值域是巴拿赫空間中的一類線性子空間。例如,巴拿赫空間中每個閉線性子空間都是運算元值域。...
閉值域定理(Closed - field theorem)是數學中的巴拿赫空間理論中的一個定理,給出了閉合稠定線性運算元(closed densely defined operator)的值域為閉集的充要條件。這...
緊運算元是一類重要的有界運算元,它最接近於有限維空間上的線性運算元。...... 巴拿赫空間,則從X到Y的緊線性運算元全體𝒦(X→Y)是巴拿赫空間𝓑(X→Y)的閉線性子...
設A是賦范線性空間X到賦范線性空間Y的有界線性運算元,如果值域𝓡(A)是Y的有限維線性子空間,則稱A是有限秩運算元。...
《現代數學基礎:泛函分析中的反例》匯集了泛函分析中的大量反例,主要內容有度量空間、賦范線性空間、線性運算元、弱拓撲和弱*拓撲、向量值函式、不動點理論、Hilbert...
泛函分析巴拿赫空間 這是最常見,套用最廣的一類拓撲線性空間。比如有限閉區間上的連續函式空間,有限閉區間上的k次可微函式空間。或者對於每個實數p,如果p ≥ 1,...
