基本介紹
- 中文名:牛頓定理
- 外文名:Newton's Theorem
- 提出者:艾薩克·牛頓
- 套用學科:數學
- 適用領域範圍:平面幾何
定理1
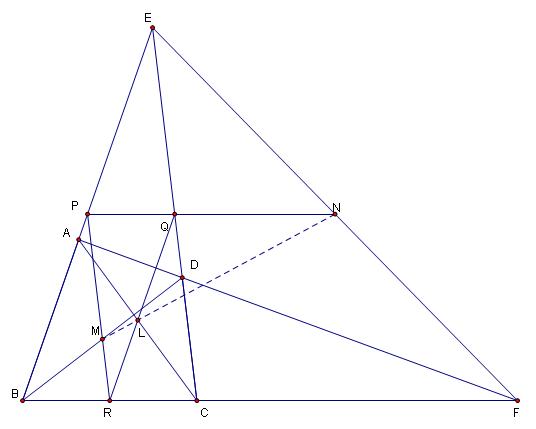 牛頓定理1
牛頓定理1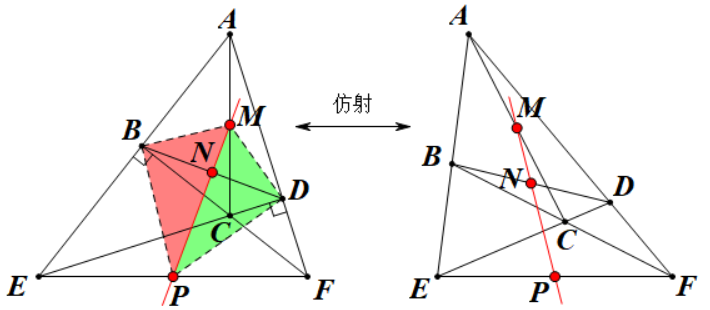 牛頓定理1仿射證明法
牛頓定理1仿射證明法定理2
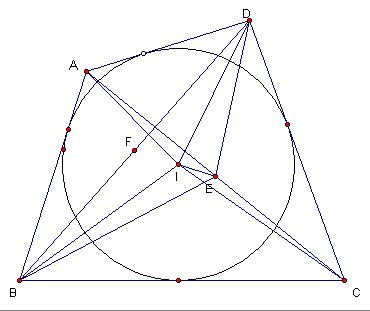 牛頓定理2圖
牛頓定理2圖定理3


 牛頓定理1
牛頓定理1 牛頓定理1仿射證明法
牛頓定理1仿射證明法 牛頓定理2圖
牛頓定理2圖
牛頓運動定律包括牛頓第一運動定律、牛頓第二運動定律和牛頓第三運動定律三條定律,由艾薩克·牛頓在1687年於《自然哲學的數學原理》一書中總結提出。其中,第一定律...
特指平面幾何中的牛頓定理(Newton's Theorem)牛頓線:和完全四邊形四邊相切的有心圓錐曲線的心的軌跡是一條直線,是完全四邊形三條對角線中點所共的線。(涵蓋了圓...
牛頓-萊布尼茲公式(Newton-Leibniz formula),通常也被稱為微積分基本定理,揭示了定積分與被積函式的原函式或者不定積分之間的聯繫。牛頓-萊布尼茨公式的內容是一個...
牛頓法最初由艾薩克·牛頓於1736年在 Method of Fluxions 中公開提出。而事實上方法此時已經由Joseph Raphson於1690年在Analysis Aequationum中提出,與牛頓法相關的...
性質 理論規律 目的 為相關理論提供數據實踐證明 出處 古希臘泰勒斯定律 目錄 1 理論規律統稱 2 漢語詞語 定律理論規律統稱 編輯 牛頓三大定律牛頓第一定律: ...
對於n次多項式F(X)有著名的牛頓恆等式。它是n次方程F(X)=0的n個根的同次冪的和與F(X)的函式之間關係的明確表述。...
二項式定理(英語:Binomial theorem),又稱牛頓二項式定理,由艾薩克·牛頓於1664年、1665年間提出。該定理給出兩個數之和的整數次冪諸如展開為類似項之和的恆等式。...
牛頓疊代法(Newton's method)又稱為牛頓-拉夫遜(拉弗森)方法(Newton-Raphson method),它是牛頓在17世紀提出的一種在實數域和複數域上近似求解方程的方法。...
動力學的普遍定理之一。內容為物體動量的增量等於它所受合外力的衝量即Ft=mΔv,即所有外力的衝量的矢量和。其定義為:如果一個系統不受外力或所受外力的矢量和...
艾薩克·牛頓(1643年1月4日—1727年3月31日)爵士,英國皇家學會會長,英國著名的物理學家,百科全書式的“全才”,著有《自然哲學的數學原理》、《光學》。他在...
任一點上的剪應力都同剪下變形速率呈線性函式關係的流體稱為牛頓流體。最簡單的牛頓流體流動是二無限平板以相對速度U相互平行運動時,兩板間粘性流體的低速定常剪下...
《牛頓定律與愛情》是寂年瞳畫創作的網路小說,發表於晉江文學網。...... 《牛頓定律與愛情》是寂年瞳畫創作的網路小說,發表於晉江文學網。中文名稱 牛頓定律與愛...
克卜勒定律數學推導 克卜勒定律是關於行星環繞太陽的運動,而牛頓定律更廣義的是關於幾個粒子因萬有引力相互吸引而產生的運動。在只有兩個粒子,其中一個粒子超輕於...
