完全四邊形是指四條直線兩兩相交,共有六個交點,這四線六點所形成的圖形。四條直線稱為它的邊,六個交點稱為它的頂點。不共邊的兩個頂點稱為對頂點,它們的連線稱為對角線。
基本介紹
- 中文名:完全四邊形
- 外文名:complete quadrangle
- 構成:四線六點
- 包含圖形:凸四邊形、凹四邊形等
- 套用:圖形幾何
- 學科:數學
定義
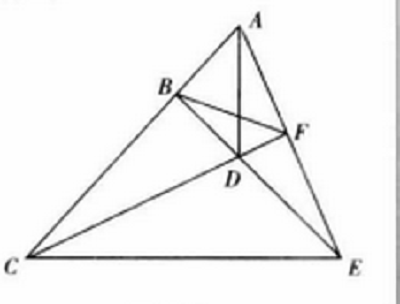 圖一
圖一
完全四邊形是指四條直線兩兩相交,共有六個交點,這四線六點所形成的圖形。四條直線稱為它的邊,六個交點稱為它的頂點。不共邊的兩個頂點稱為對頂點,它們的連線稱為對角線。
 圖一
圖一完全四邊形是指四條直線兩兩相交,共有六個交點,這四線六點所形成的圖形。四條直線稱為它的邊,六個交點稱為它的頂點。不共邊的兩個頂點稱為對頂點,它們的...
在數學,尤其是射影幾何學裡,完全四線形是指歐幾里德平面上由四條兩兩相交但是任意三條不共點的直線加上它們的六個交點組成的圖形。相應地,由四個三三不共線...
特指平面幾何中的牛頓定理(Newton's Theorem)牛頓線:和完全四邊形四邊相切的有心圓錐曲線的心的軌跡是一條直線,是完全四邊形三條對角線中點所共的線。(涵蓋了圓...
密克爾點(Miquel點又譯:米格爾點、密克點或米庫爾點):來自密克爾定理中的完全四邊形定理:如果ABCDEF是完全四邊形,那么三角形△EAD,△EBC,△FAB,△FDC的外接圓交...
(完全四邊形的密克定理) 四條兩兩相交的直線形成四個三角形,它們的外接圓共點 [2] 。米奎爾定理推論2 在△ABC中,點D、E、F分別在邊BC、CA、AB上,設M為其...
四垂心共線作者:夏培貴 引理如圖 1(1)、(2),若AD∥BE,BD∥CE,且AD/BE=BD/CE,則A、B、C三點共線。 這不會有異議,就免去論證。定理完全四邊形中的四...
規形定理(theorem of compasses form)是在完全四邊形邊上求分點比值的定理。在折線BAC的BA,AC兩線段上各取一點D、E,設CD,BE交於點F,若BD=DA=1∶λ,CE∶...
例3 四條直線AE、AF、ED、FB兩兩相交成四個三角形,它們的四個外接圓ABF、BCE,CDF及DAE共點。這點叫做四條直線所構成的完全四邊形的密克點(Miquel)。...
如果ABCDEF是完全四邊形,那么三角形的外接圓交於一點 O,稱為密克點。密克定理四圓定理 設C1, C2,C3, C4為四個圓,A1和B1是C1和C2的交點,A2和B2是C2 和C3...
完全四邊形:兩兩相交又無三線共點的四條直線及它們的六個交點所構成的圖形稱為完全四邊形。 三角形等角共軛點:與三角形的邊所成的角對應相等的一對點。...
由四條直線(其中無三線共點)以及其中任意兩條直線的六個交點所組成的圖形叫完全四邊形(右圖b)。這四條直線叫邊,六個點叫頂點,不在公共邊上的兩頂點叫對頂,...
79. 完全四邊形 80. 分點公式 81. 以一當二 82. Simson線 83. 謬論一例 84. 根軸 85. 重要之點 86. 合二為一 87. 一道題的純幾何證明 88. 充分...
極圓(polar circle)是以三角形的垂心為中心、以這一三角形為自配極三角形的...定理6 完全四邊形的各個三角形的極圓,組成共軸圓組,與以對角線為直徑的圓...
與此同時,他還引入了“完全四邊形”的術語。中文名 拉扎爾·卡諾 外文名 Carnot, Lazare Nicolas Marguerite 出生日期 1753 逝世日期 1823 ...
8. 完全四邊形、調和點列9. 反演與配極10. 幾何不等式11. 平面幾何中的其他方法和問題選講習題解答參考資料 1. 奧數小叢書(第二版)高中卷7(平面幾何) ....
6.2四邊形中有向面積的定值定理及其套用 6.2.1四邊形中邊三角形和對角線分點三角形有向面積的定值定理及其套用 6.2.2完全四邊形中有向面積的定值定理及...
他建立射影幾何的嚴密系統,推廣卡諾(Carnot)完全四邊形的工作到空間多邊形去,完成了點列、線束、二次曲線及曲面的理論,討論圓錐曲線和“帕斯卡六角形”的種種性質。...
四邊形坎迪定理推廣 // 證法153說明3,4,5四邊形蝴蝶定理 // 證法153說明4,5四邊形蝴蝶定理推廣 // 證法153說明4,5完全四邊形蝴蝶定理 // 證法153說明3,...
《幾何瑰寶》共有三角形、幾何變換,三角形、圓,四邊形、圓,多邊形、圓,以及最值,作圖,軌跡,完全四邊形,平面閉折線,圓的推廣十個專題,對平面幾何中的500餘顆...
若作一圓錐曲線的內接四邊形,則任一不過頂點的直線與圓錐曲線以及與完全四邊形對邊相交的四對點有對合關係,這就是著名的德扎格對合定理.德扎格還引人了調和點...
他建立射影幾何的嚴密系統,推廣卡諾完全四邊形的工作到空間多邊形上去,完成了點列、線束、二次曲線及曲面的理論,討論圓錐曲線和“帕斯卡六角形”的性質。由於他在...
