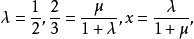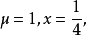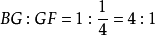規形定理(theorem of compasses form)是在完全四邊形邊上求分點比值的定理。在折線BAC的BA,AC兩線段上各取一點D、E,設CD,BE交於點F,若BD=DA=1∶λ,CE∶EA=1∶μ,則必BF∶FE= 1∶(λ/(1+μ)),CF∶FD= 1∶(μ/(1+λ)) 。
基本介紹
- 中文名:規形定理
- 外文名:theorem of compasses form
- 所屬學科:數學
- 所屬問題:平面幾何
- 套用:在完全四邊形邊上求分點比值
定理介紹,規形定理的證明,規形定理的說明,規形定理的套用,
定理介紹
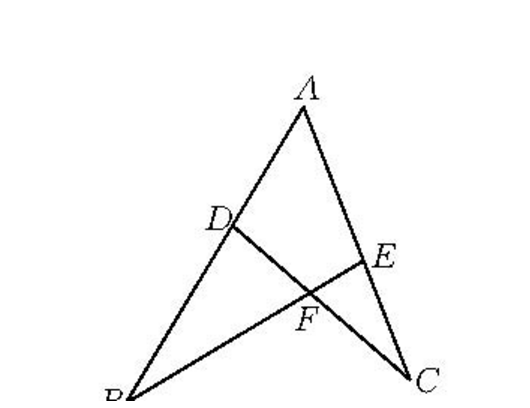
規形定理 如圖1,完全四邊形ADFEBC中,在折線BAC的BA,AC兩線段上各取一點D、E,設CD,BE交於點F,若BD=DA=1∶λ,CE∶EA=1∶μ,則必
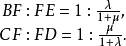
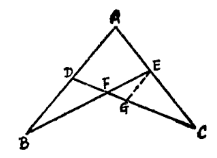 圖1
圖1套用此定理對形如二腳規的凹四邊形在已知部分分點所得比值的情況下,可求出另外分點的比值。
規形定理的證明
證明 如圖1,過E引EG//AB,且交DC於G、注意△EGF∽△BDF及△CEG∽△CAD,有
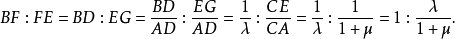
同理可證另一式。
規形定理的說明
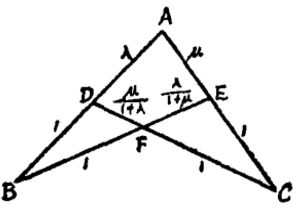 圖2
圖2說明:
(1) 規形定理可以用圖2表示。我們在BD邊上標出1,DA邊上標出λ……,不表示BD長為1,DA長為λ,只表示在同一直線上的兩線段的比例數,即指BD:DA=1:λ。
(2) 由於圖2外形像一隻二腳規,故稱文中定理為“規形定理”,規形外殼為一凹四邊形,可稱圖2為規形FCAB。
(3) 必須熟記圖2中各線段的比例數,其中特別注意從“足尖" B、C出發的四條線段的比例數均定為1。
規形定理的套用
下面舉例來說明” 規形定理”的套用。
【例1】在△ABC的BC和CA邊上分別取P,Q,使BP:PC=1:2,CQ:QA=2:3,連AP,BQ交於R,求AR:RP是多少?
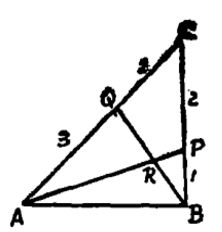 圖3
圖3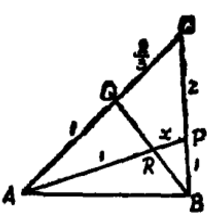 圖4
圖4解:依題意作出圖3,與圖2對照,把各比例數標準化得圖4,此處的標準化,是指從“足尖”出發的各線段的比例數均要定為1 (注意:當AQ的比例數定為1時,QC的比例數就為2/3),令AR:RP=1:x,則依規形定理,有:


【例2】在△ABC中, D在AB上,且使AD:DB=1:2,而G在CD上,且使CG:GD=3:2,如果BG交AC於F,求BG:GF?
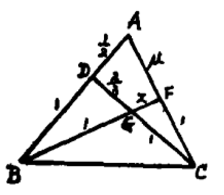 圖5
圖5解:依題意作出圖5,其中規形GBAC的各比例數已標準化,即得: